mathematics definition essay

“What is Mathematics?” and why we should ask, where one should experience and learn that, and how to teach it

• Conference paper
• Open Access
• First Online: 02 November 2017
• Cite this conference paper

You have full access to this open access conference paper

• Günter M. Ziegler 3 &
• Andreas Loos 4  

Part of the book series: ICME-13 Monographs ((ICME13Mo))

113k Accesses

10 Citations

3 Altmetric

“What is Mathematics?” [with a question mark!] is the title of a famous book by Courant and Robbins, first published in 1941, which does not answer the question. The question is, however, essential: The public image of the subject (of the science, and of the profession) is not only relevant for the support and funding it can get, but it is also crucial for the talent it manages to attract—and thus ultimately determines what mathematics can achieve, as a science, as a part of human culture, but also as a substantial component of economy and technology. In this lecture we thus

discuss the image of mathematics (where “image” might be taken literally!),

sketch a multi-facetted answer to the question “What is Mathematics?,”

stress the importance of learning “What is Mathematics” in view of Klein’s “double discontinuity” in mathematics teacher education,

present the “Panorama project” as our response to this challenge,

stress the importance of telling stories in addition to teaching mathematics, and finally,

suggest that the mathematics curricula at schools and at universities should correspondingly have space and time for at least three different subjects called Mathematics.

This paper is a slightly updated reprint of: Günter M. Ziegler and Andreas Loos, Learning and Teaching “ What is Mathematics ”, Proc. International Congress of Mathematicians, Seoul 2014, pp. 1201–1215; reprinted with kind permission by Prof. Hyungju Park, the chairman of ICM 2014 Organizing Committee.

You have full access to this open access chapter,  Download conference paper PDF

Similar content being viewed by others

The Missing Element for Teachers: Learning What Mathematics Is

Educational Paths to Mathematics: Which Paths Forward to What Mathematics?

Mathematics at the Center of Distinct Fields: A Response to Michael and Ted

What is mathematics.

Defining mathematics. According to Wikipedia in English, in the March 2014 version, the answer to “What is Mathematics?” is

Mathematics is the abstract study of topics such as quantity (numbers), [2] structure, [3] space, [2] and change. [4][5][6] There is a range of views among mathematicians and philosophers as to the exact scope and definition of mathematics. [7][8] Mathematicians seek out patterns (Highland & Highland, 1961 , 1963 ) and use them to formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proof. When mathematical structures are good models of real phenomena, then mathematical reasoning can provide insight or predictions about nature. Through the use of abstraction and logic, mathematics developed from counting, calculation, measurement, and the systematic study of the shapes and motions of physical objects. Practical mathematics has been a human activity for as far back as written records exist. The research required to solve mathematical problems can take years or even centuries of sustained inquiry.

None of this is entirely wrong, but it is also not satisfactory. Let us just point out that the fact that there is no agreement about the definition of mathematics, given as part of a definition of mathematics, puts us into logical difficulties that might have made Gödel smile. Footnote 1

The answer given by Wikipedia in the current German version, reads (in our translation):

Mathematics […] is a science that developed from the investigation of geometric figures and the computing with numbers. For mathematics , there is no commonly accepted definition; today it is usually described as a science that investigates abstract structures that it created itself by logical definitions using logic for their properties and patterns.

This is much worse, as it portrays mathematics as a subject without any contact to, or interest from, a real world.

The borders of mathematics. Is mathematics “stand-alone”? Could it be defined without reference to “neighboring” subjects, such as physics (which does appear in the English Wikipedia description)? Indeed, one possibility to characterize mathematics describes the borders/boundaries that separate it from its neighbors. Even humorous versions of such “distinguishing statements” such as

“Mathematics is the part of physics where the experiments are cheap.”

“Mathematics is the part of philosophy where (some) statements are true—without debate or discussion.”

“Mathematics is computer science without electricity.” (So “Computer science is mathematics with electricity.”)

contain a lot of truth and possibly tell us a lot of “characteristics” of our subject. None of these is, of course, completely true or completely false, but they present opportunities for discussion.

What we do in mathematics . We could also try to define mathematics by “what we do in mathematics”: This is much more diverse and much more interesting than the Wikipedia descriptions! Could/should we describe mathematics not only as a research discipline and as a subject taught and learned at school, but also as a playground for pupils, amateurs, and professionals, as a subject that presents challenges (not only for pupils, but also for professionals as well as for amateurs), as an arena for competitions, as a source of problems, small and large, including some of the hardest problems that science has to offer, at all levels from elementary school to the millennium problems (Csicsery, 2008 ; Ziegler, 2011 )?

What we teach in mathematics classes . Education bureaucrats might (and probably should) believe that the question “What is Mathematics?” is answered by high school curricula. But what answers do these give?

This takes us back to the nineteenth century controversies about what mathematics should be taught at school and at the Universities. In the German version this was a fierce debate. On the one side it saw the classical educational ideal as formulated by Wilhelm von Humboldt (who was involved in the concept for and the foundation 1806 of the Berlin University, now named Humboldt Universität, and to a certain amount shaped the modern concept of a university); here mathematics had a central role, but this was the classical “Greek” mathematics, starting from Euclid’s axiomatic development of geometry, the theory of conics, and the algebra of solving polynomial equations, not only as cultural heritage, but also as a training arena for logical thinking and problem solving. On the other side of the fight were the proponents of “Realbildung”: Realgymnasien and the technical universities that were started at that time tried to teach what was needed in commerce and industry: calculation and accounting, as well as the mathematics that could be useful for mechanical and electrical engineering—second rate education in the view of the classical German Gymnasium.

This nineteenth century debate rests on an unnatural separation into the classical, pure mathematics, and the useful, applied mathematics; a division that should have been overcome a long time ago (perhaps since the times of Archimedes), as it is unnatural as a classification tool and it is also a major obstacle to progress both in theory and in practice. Nevertheless the division into “classical” and “current” material might be useful in discussing curriculum contents—and the question for what purpose it should be taught; see our discussion in the Section “ Three Times Mathematics at School? ”.

The Courant–Robbins answer . The title of the present paper is, of course, borrowed from the famous and very successful book by Richard Courant and Herbert Robbins. However, this title is a question—what is Courant and Robbins’ answer? Indeed, the book does not give an explicit definition of “What is Mathematics,” but the reader is supposed to get an idea from the presentation of a diverse collection of mathematical investigations. Mathematics is much bigger and much more diverse than the picture given by the Courant–Robbins exposition. The presentation in this section was also meant to demonstrate that we need a multi-facetted picture of mathematics: One answer is not enough, we need many.

Why Should We Care?

The question “What is Mathematics?” probably does not need to be answered to motivate why mathematics should be taught, as long as we agree that mathematics is important.

However, a one-sided answer to the question leads to one-sided concepts of what mathematics should be taught.

At the same time a one-dimensional picture of “What is Mathematics” will fail to motivate kids at school to do mathematics, it will fail to motivate enough pupils to study mathematics, or even to think about mathematics studies as a possible career choice, and it will fail to motivate the right students to go into mathematics studies, or into mathematics teaching. If the answer to the question “What is Mathematics”, or the implicit answer given by the public/prevailing image of the subject, is not attractive, then it will be very difficult to motivate why mathematics should be learned—and it will lead to the wrong offers and the wrong choices as to what mathematics should be learned.

Indeed, would anyone consider a science that studies “abstract” structures that it created itself (see the German Wikipedia definition quoted above) interesting? Could it be relevant? If this is what mathematics is, why would or should anyone want to study this, get into this for a career? Could it be interesting and meaningful and satisfying to teach this?

Also in view of the diversity of the students’ expectations and talents, we believe that one answer is plainly not enough. Some students might be motivated to learn mathematics because it is beautiful, because it is so logical, because it is sometimes surprising. Or because it is part of our cultural heritage. Others might be motivated, and not deterred, by the fact that mathematics is difficult. Others might be motivated by the fact that mathematics is useful, it is needed—in everyday life, for technology and commerce, etc. But indeed, it is not true that “the same” mathematics is needed in everyday life, for university studies, or in commerce and industry. To other students, the motivation that “it is useful” or “it is needed” will not be sufficient. All these motivations are valid, and good—and it is also totally valid and acceptable that no single one of these possible types of arguments will reach and motivate all these students.

Why do so many pupils and students fail in mathematics, both at school and at universities? There are certainly many reasons, but we believe that motivation is a key factor. Mathematics is hard. It is abstract (that is, most of it is not directly connected to everyday-life experiences). It is not considered worth-while. But a lot of the insufficient motivation comes from the fact that students and their teachers do not know “What is Mathematics.”

Thus a multi-facetted image of mathematics as a coherent subject, all of whose many aspects are well connected, is important for a successful teaching of mathematics to students with diverse (possible) motivations.

This leads, in turn, to two crucial aspects, to be discussed here next: What image do students have of mathematics? And then, what should teachers answer when asked “What is Mathematics”? And where and how and when could they learn that?

The Image of Mathematics

A 2008 study by Mendick, Epstein, and Moreau ( 2008 ), which was based on an extensive survey among British students, was summarized as follows:

Many students and undergraduates seem to think of mathematicians as old, white, middle-class men who are obsessed with their subject, lack social skills and have no personal life outside maths. The student’s views of maths itself included narrow and inaccurate images that are often limited to numbers and basic arithmetic.

The students’ image of what mathematicians are like is very relevant and turns out to be a massive problem, as it defines possible (anti-)role models, which are crucial for any decision in the direction of “I want to be a mathematician.” If the typical mathematician is viewed as an “old, white, male, middle-class nerd,” then why should a gifted 16-year old girl come to think “that’s what I want to be when I grow up”? Mathematics as a science, and as a profession, looses (or fails to attract) a lot of talent this way! However, this is not the topic of this presentation.

On the other hand the first and the second diagnosis of the quote from Mendick et al. ( 2008 ) belong together: The mathematicians are part of “What is Mathematics”!

And indeed, looking at the second diagnosis, if for the key word “mathematics” the images that spring to mind don’t go beyond a per se meaningless “ \( a^{2} + b^{2} = c^{2} \) ” scribbled in chalk on a blackboard—then again, why should mathematics be attractive, as a subject, as a science, or as a profession?

We think that we have to look for, and work on, multi-facetted and attractive representations of mathematics by images. This could be many different, separate images, but this could also be images for “mathematics as a whole.”

Four Images for “What Is Mathematics?”

Striking pictorial representations of mathematics as a whole (as well as of other sciences!) and of their change over time can be seen on the covers of the German “Was ist was” books. The history of these books starts with the series of “How and why” Wonder books published by Grosset and Dunlop, New York, since 1961, which was to present interesting subjects (starting with “Dinosaurs,” “Weather,” and “Electricity”) to children and younger teenagers. The series was published in the US and in Great Britain in the 1960s and 1970s, but it was and is much more successful in Germany, where it was published (first in translation, then in volumes written in German) by Ragnar Tessloff since 1961. Volume 18 in the US/UK version and Volume 12 in the German version treats “Mathematics”, first published in 1963 (Highland & Highland, 1963 ), but then republished with the same title but a new author and contents in 2001 (Blum, 2001 ). While it is worthwhile to study the contents and presentation of mathematics in these volumes, we here focus on the cover illustrations (see Fig.  1 ), which for the German edition exist in four entirely different versions, the first one being an adaption of the original US cover of (Highland & Highland, 1961 ).

The four covers of “Was ist was. Band 12: Mathematik” (Highland & Highland, 1963 ; Blum, 2001 )

All four covers represent a view of “What is Mathematics” in a collage mode, where the first one represents mathematics as a mostly historical discipline (starting with the ancient Egyptians), while the others all contain a historical allusion (such as pyramids, Gauß, etc.) alongside with objects of mathematics (such as prime numbers or \( \pi \) , dices to illustrate probability, geometric shapes). One notable object is the oddly “two-colored” Möbius band on the 1983 cover, which was changed to an entirely green version in a later reprint.

One can discuss these covers with respect to their contents and their styles, and in particular in terms of attractiveness to the intended buyers/readers. What is over-emphasized? What is missing? It seems more important to us to

think of our own images/representations for “What is Mathematics”,

think about how to present a multi-facetted image of “What is Mathematics” when we teach.

Indeed, the topics on the covers of the “Was ist was” volumes of course represent interesting (?) topics and items discussed in the books. But what do they add up to? We should compare this to the image of mathematics as represented by school curricula, or by the university curricula for teacher students.

In the context of mathematics images, let us mention two substantial initiatives to collect and provide images from current mathematics research, and make them available on internet platforms, thus providing fascinating, multi-facetted images of mathematics as a whole discipline:

Guy Métivier et al.: “Image des Maths. La recherche mathématique en mots et en images” [“Images of Maths. Mathematical research in words and images”], CNRS, France, at images.math.cnrs.fr (texts in French)

Andreas D. Matt, Gert-Martin Greuel et al.: “IMAGINARY. open mathematics,” Mathematisches Forschungsinstitut Oberwolfach, at imaginary.org (texts in German, English, and Spanish).

The latter has developed from a very successful travelling exhibition of mathematics images, “IMAGINARY—through the eyes of mathematics,” originally created on occasion of and for the German national science year 2008 “Jahr der Mathematik. Alles was zählt” [“Year of Mathematics 2008. Everything that counts”], see www.jahr-der-mathematik.de , which was highly successful in communicating a current, attractive image of mathematics to the German public—where initiatives such as the IMAGINARY exhibition had a great part in the success.

Teaching “What Is Mathematics” to Teachers

More than 100 years ago, in 1908, Felix Klein analyzed the education of teachers. In the introduction to the first volume of his “Elementary Mathematics from a Higher Standpoint” he wrote (our translation):

At the beginning of his university studies, the young student is confronted with problems that do not remind him at all of what he has dealt with up to then, and of course, he forgets all these things immediately and thoroughly. When after graduation he becomes a teacher, he has to teach exactly this traditional elementary mathematics, and since he can hardly link it with his university mathematics, he soon readopts the former teaching tradition and his studies at the university become a more or less pleasant reminiscence which has no influence on his teaching (Klein, 1908 ).

This phenomenon—which Klein calls the double discontinuity —can still be observed. In effect, the teacher students “tunnel” through university: They study at university in order to get a degree, but nevertheless they afterwards teach the mathematics that they had learned in school, and possibly with the didactics they remember from their own school education. This problem observed and characterized by Klein gets even worse in a situation (which we currently observe in Germany) where there is a grave shortage of Mathematics teachers, so university students are invited to teach at high school long before graduating from university, so they have much less university education to tunnel at the time when they start to teach in school. It may also strengthen their conviction that University Mathematics is not needed in order to teach.

How to avoid the double discontinuity is, of course, a major challenge for the design of university curricula for mathematics teachers. One important aspect however, is tied to the question of “What is Mathematics?”: A very common highschool image/concept of mathematics, as represented by curricula, is that mathematics consists of the subjects presented by highschool curricula, that is, (elementary) geometry, algebra (in the form of arithmetic, and perhaps polynomials), plus perhaps elementary probability, calculus (differentiation and integration) in one variable—that’s the mathematics highschool students get to see, so they might think that this is all of it! Could their teachers present them a broader picture? The teachers after their highschool experience studied at university, where they probably took courses in calculus/analysis, linear algebra, classical algebra, plus some discrete mathematics, stochastics/probability, and/or numerical analysis/differential equations, perhaps a programming or “computer-oriented mathematics” course. Altogether they have seen a scope of university mathematics where no current research becomes visible, and where most of the contents is from the nineteenth century, at best. The ideal is, of course, that every teacher student at university has at least once experienced how “doing research on your own” feels like, but realistically this rarely happens. Indeed, teacher students would have to work and study and struggle a lot to see the fascination of mathematics on their own by doing mathematics; in reality they often do not even seriously start the tour and certainly most of them never see the “glimpse of heaven.” So even if the teacher student seriously immerges into all the mathematics on the university curriculum, he/she will not get any broader image of “What is Mathematics?”. Thus, even if he/she does not tunnel his university studies due to the double discontinuity, he/she will not come back to school with a concept that is much broader than that he/she originally gained from his/her highschool times.

Our experience is that many students (teacher students as well as classical mathematics majors) cannot name a single open problem in mathematics when graduating the university. They have no idea of what “doing mathematics” means—for example, that part of this is a struggle to find and shape the “right” concepts/definitions and in posing/developing the “right” questions and problems.

And, moreover, also the impressions and experiences from university times will get old and outdated some day: a teacher might be active at a school for several decades—while mathematics changes! Whatever is proved in mathematics does stay true, of course, and indeed standards of rigor don’t change any more as much as they did in the nineteenth century, say. However, styles of proof do change (see: computer-assisted proofs, computer-checkable proofs, etc.). Also, it would be good if a teacher could name “current research focus topics”: These do change over ten or twenty years. Moreover, the relevance of mathematics in “real life” has changed dramatically over the last thirty years.

The Panorama Project

For several years, the present authors have been working on developing a course [and eventually a book (Loos & Ziegler, 2017 )] called “Panorama der Mathematik” [“Panorama of Mathematics”]. It primarily addresses mathematics teacher students, and is trying to give them a panoramic view on mathematics: We try to teach an overview of the subject, how mathematics is done, who has been and is doing it, including a sketch of main developments over the last few centuries up to the present—altogether this is supposed to amount to a comprehensive (but not very detailed) outline of “What is Mathematics.” This, of course, turns out to be not an easy task, since it often tends to feel like reading/teaching poetry without mastering the language. However, the approach of Panorama is complementing mathematics education in an orthogonal direction to the classic university courses, as we do not teach mathematics but present (and encourage to explore ); according to the response we get from students they seem to feel themselves that this is valuable.

Our course has many different components and facets, which we here cast into questions about mathematics. All these questions (even the ones that “sound funny”) should and can be taken seriously, and answered as well as possible. For each of them, let us here just provide at most one line with key words for answers:

When did mathematics start?

Numbers and geometric figures start in stone age; the science starts with Euclid?

How large is mathematics? How many Mathematicians are there?

The Mathematics Genealogy Project had 178854 records as of 12 April 2014.

How is mathematics done, what is doing research like?

Collect (auto)biographical evidence! Recent examples: Frenkel ( 2013 ) , Villani ( 2012 ).

What does mathematics research do today? What are the Grand Challenges?

The Clay Millennium problems might serve as a starting point.

What and how many subjects and subdisciplines are there in mathematics?

See the Mathematics Subject Classification for an overview!

Why is there no “Mathematical Industry”, as there is e.g. Chemical Industry?

There is! See e.g. Telecommunications, Financial Industry, etc.

What are the “key concepts” in mathematics? Do they still “drive research”?

Numbers, shapes, dimensions, infinity, change, abstraction, …; they do.

What is mathematics “good for”?

It is a basis for understanding the world, but also for technological progress.

Where do we do mathematics in everyday life?

Not only where we compute, but also where we read maps, plan trips, etc.

Where do we see mathematics in everyday life?

There is more maths in every smart phone than anyone learns in school.

What are the greatest achievements of mathematics through history?

Make your own list!

An additional question is how to make university mathematics more “sticky” for the tunneling teacher students, how to encourage or how to force them to really connect to the subject as a science. Certainly there is no single, simple, answer for this!

Telling Stories About Mathematics

How can mathematics be made more concrete? How can we help students to connect to the subject? How can mathematics be connected to the so-called real world?

Showing applications of mathematics is a good way (and a quite beaten path). Real applications can be very difficult to teach since in most advanced, realistic situation a lot of different mathematical disciplines, theories and types of expertise have to come together. Nevertheless, applications give the opportunity to demonstrate the relevance and importance of mathematics. Here we want to emphasize the difference between teaching a topic and telling about it. To name a few concrete topics, the mathematics behind weather reports and climate modelling is extremely difficult and complex and advanced, but the “basic ideas” and simplified models can profitably be demonstrated in highschool, and made plausible in highschool level mathematical terms. Also success stories like the formula for the Google patent for PageRank (Page, 2001 ), see Langville and Meyer ( 2006 ), the race for the solution of larger and larger instances of the Travelling Salesman Problem (Cook, 2011 ), or the mathematics of chip design lend themselves to “telling the story” and “showing some of the maths” at a highschool level; these are among the topics presented in the first author’s recent book (Ziegler, 2013b ), where he takes 24 images as the starting points for telling stories—and thus developing a broader multi-facetted picture of mathematics.

Another way to bring maths in contact with non-mathematicians is the human level. Telling stories about how maths is done and by whom is a tricky way, as can be seen from the sometimes harsh reactions on www.mathoverflow.net to postings that try to excavate the truth behind anecdotes and legends. Most mathematicians see mathematics as completely independent from the persons who explored it. History of mathematics has the tendency to become gossip , as Gian-Carlo Rota once put it (Rota, 1996 ). The idea seems to be: As mathematics stands for itself, it has also to be taught that way.

This may be true for higher mathematics. However, for pupils (and therefore, also for teachers), transforming mathematicians into humans can make science more tangible, it can make research interesting as a process (and a job?), and it can be a starting/entry point for real mathematics. Therefore, stories can make mathematics more sticky. Stories cannot replace the classical approaches to teaching mathematics. But they can enhance it.

Stories are the way by which knowledge has been transferred between humans for thousands of years. (Even mathematical work can be seen as a very abstract form of storytelling from a structuralist point of view.) Why don’t we try to tell more stories about mathematics, both at university and in school—not legends, not fairy tales, but meta-information on mathematics—in order to transport mathematics itself? See (Ziegler, 2013a ) for an attempt by the first author in this direction.

By stories, we do not only mean something like biographies, but also the way of how mathematics is created or discovered: Jack Edmonds’ account (Edmonds, 1991 ) of how he found the blossom shrink algorithm is a great story about how mathematics is actually done . Think of Thomas Harriot’s problem about stacking cannon balls into a storage space and what Kepler made out of it: the genesis of a mathematical problem. Sometimes scientists even wrap their work into stories by their own: see e.g. Leslie Lamport’s Byzantine Generals (Lamport, Shostak, & Pease, 1982 ).

Telling how research is done opens another issue. At school, mathematics is traditionally taught as a closed science. Even touching open questions from research is out of question, for many good and mainly pedagogical reasons. However, this fosters the image of a perfect science where all results are available and all problems are solved—which is of course completely wrong (and moreover also a source for a faulty image of mathematics among undergraduates).

Of course, working with open questions in school is a difficult task. None of the big open questions can be solved with an elementary mathematical toolbox; many of them are not even accessible as questions. So the big fear of discouraging pupils is well justified. On the other hand, why not explore mathematics by showing how questions often pop up on the way? Posing questions in and about mathematics could lead to interesting answers—in particular to the question of “What is Mathematics, Really?”

Three Times Mathematics at School?

So, what is mathematics? With school education in mind, the first author has argued in Ziegler ( 2012 ) that we are trying cover three aspects the same time, which one should consider separately and to a certain extent also teach separately:

A collection of basic tools, part of everyone’s survival kit for modern-day life—this includes everything, but actually not much more than, what was covered by Adam Ries’ “Rechenbüchlein” [“Little Book on Computing”] first published in 1522, nearly 500 years ago;

A field of knowledge with a long history, which is a part of our culture and an art, but also a very productive basis (indeed a production factor) for all modern key technologies. This is a “story-telling” subject.

An introduction to mathematics as a science—an important, highly developed, active, huge research field.

Looking at current highschool instruction, there is still a huge emphasis on Mathematics I, with a rather mechanical instruction on arithmetic, “how to compute correctly,” and basic problem solving, plus a rather formal way of teaching Mathematics III as a preparation for possible university studies in mathematics, sciences or engineering. Mathematics II, which should provide a major component of teaching “What is Mathematics,” is largely missing. However, this part also could and must provide motivation for studying Mathematics I or III!

What Is Mathematics, Really?

There are many, and many different, valid answers to the Courant-Robbins question “What is Mathematics?”

A more philosophical one is given by Reuben Hersh’s book “What is Mathematics, Really?” Hersh ( 1997 ), and there are more psychological ones, on the working level. Classics include Jacques Hadamard’s “Essay on the Psychology of Invention in the Mathematical Field” and Henri Poincaré’s essays on methodology; a more recent approach is Devlin’s “Introduction to Mathematical Thinking” Devlin ( 2012 ), or Villani’s book ( 2012 ).

And there have been many attempts to describe mathematics in encyclopedic form over the last few centuries. Probably the most recent one is the gargantuan “Princeton Companion to Mathematics”, edited by Gowers et al. ( 2008 ), which indeed is a “Princeton Companion to Pure Mathematics.”

However, at a time where ZBMath counts more than 100,000 papers and books per year, and 29,953 submissions to the math and math-ph sections of arXiv.org in 2016, it is hopeless to give a compact and simple description of what mathematics really is, even if we had only the “current research discipline” in mind. The discussions about the classification of mathematics show how difficult it is to cut the science into slices, and it is even debatable whether there is any meaningful way to separate applied research from pure mathematics.

Probably the most diplomatic way is to acknowledge that there are “many mathematics.” Some years ago Tao ( 2007 ) gave an open list of mathematics that is/are good for different purposes—from “problem-solving mathematics” and “useful mathematics” to “definitive mathematics”, and wrote:

As the above list demonstrates, the concept of mathematical quality is a high-dimensional one, and lacks an obvious canonical total ordering. I believe this is because mathematics is itself complex and high-dimensional, and evolves in unexpected and adaptive ways; each of the above qualities represents a different way in which we as a community improve our understanding and usage of the subject.

In this sense, many answers to “What is Mathematics?” probably show as much about the persons who give the answers as they manage to characterize the subject.

According to Wikipedia , the same version, the answer to “Who is Mathematics” should be:

Mathematics , also known as Allah Mathematics , (born: Ronald Maurice Bean [1] ) is a hip hop producer and DJ for the Wu-Tang Clan and its solo and affiliate projects. This is not the mathematics we deal with here.

Blum, W. (2001). Was ist was. Band 12: Mathematik , Tessloff Verlag, Nürnberg. Revised version, with new cover, 2010.

Google Scholar  

Cook, W. (2011). In pursuit of the traveling salesman: Mathematics at the limits of computation . Princeton NJ: Princeton University Press.

Courant, R., & Robbins, H. (1941). What is mathematics? an elementary approach to ideas and methods (2nd ed.), Oxford: Oxford University Press. Stewart, I (ed), 1996.

Csicsery, G. (2008). Hard problems. the road to the world’s toughest math contest , Documentary film, 82 minutes (feature)/45 minutes (classroom version), Washington, DC: Mathematical Association of America.

Devlin, K. J. (2012). Introduction to mathematical thinking , published by Keith Devlin, Palo Alto CA.

Edmonds, J. (1991). A glimpse of heaven, In: J. K. Lenstra, A. Schrijver, & A. Rinnooy Kan (eds.) History of mathematical programming—A collection of personal reminiscences (pp. 32–54). Amsterdam: CWI and North-Holland.

Frenkel, E. (2013). Love & math. The heart of hidden reality . Philadelphia PA: Basic Books/Perseus Books.

Gowers, Timothy, Leader, Imre, & Barrow-Green, June (Eds.). (2008). The princeton companion to mathematics . Princeton NJ: Princeton University Press.

Highland, E. H., & Highland, H. J. (1961). The how and why wonder book of mathematics . New York: Grosset & Dunlop.

Highland, E. H., & Highland, H. J. (1963). Was ist was. Band 12: Mathematik , Neuer Tessloff Verlag, Hamburg, 1963. Revised edition 1969. New cover 1983.

Hersh, R. (1997). What is mathematics, really? . Oxford: Oxford University Press.

Klein, F.(1933). Elementarmathematik vom höheren Standpunkte aus. Teil I: Arithmetik, Algebra, Analysis , B. G. Teubner, Leipzig, 1908. Vierte Auflage. Heidelberg: Springer.

Lamport, L., Shostak, R., & Pease, M. (1982). The byzantine generals problem. ACM Transactions on Programming Languages and Systems, 4, 382–401.

Article   Google Scholar  

Langville, A. N., & Meyer, C. D. (2006). Google’s pagerank and beyond. The science of search engine rankings . Princeton and Oxford: Princeton University Press.

Loos, A., & Ziegler, G. M. (2017). Panorama der Mathematik . Heidelberg: Springer Spectrum, to appear.

Mendick, H., Epstein, D., & Moreau, M.-P. (2008). Mathematical images and identities: Education, entertainment, social justice . London: Institute for Policy Studies in Education, London Metropolitan University.

Page, L. (2001) Method for node ranking in a linked database , United States Patent No. US 6,285,999 B1, (submitted: January 9, 1998), http://www.google.com/patents/US6285999

Rota, G.-C. (1996). Indiscrete thoughts . Basel: Birkhäuser.

Tao, T. (2007). What is good mathematics? Bulletin of the American Mathematical Society, 44 (4), 623–634.

Villani, C. (2012). Théorème vivant . Paris: Bernard Grasset. (in French).

Ziegler, G. M. (2011). Three competitions. In D. Schleicher & M. Lackmann (Eds.), Invitation to mathematics. From competition to research (pp. 195–205). Berlin: Springer.

Chapter   Google Scholar  

Ziegler, G. M. (2012). Mathematics school education provides answers—To which questions? EMS Newsletter (84), 8–11.

Ziegler, G. M.(2013a). Do I count? stories from mathematics , Boca Raton FL: CRC Press/Taylor & Francis. English translation of “Darf ich Zahlen? Geschichten aus der Mathematik”, Piper, München, 2010.

Ziegler, G. M. (2013b). Mathematik—Das ist doch keine Kunst! . München: Knaus.

Download references

Acknowledgment

The authors’ work has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 247029, the DFG Research Center Matheon, and the the DFG Collaborative Research Center TRR 109 “Discretization in Geometry and Dynamics”.

Author information

Authors and affiliations.

Institut Für Mathematik, FU Berlin, Arnimallee 2, 14195, Berlin, Germany

Günter M. Ziegler

Zeit Online, Askanischer Platz 1, 10963, Berlin, Germany

Andreas Loos

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Günter M. Ziegler .

Editor information

Editors and affiliations.

Faculty of Education, Universität Hamburg, Hamburg, Hamburg, Germany

Gabriele Kaiser

Rights and permissions

Open Access Except where otherwise noted, this chapter is licensed under a Creative Commons Attribution 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

Copyright information

© 2017 The Author(s)

About this paper

Cite this paper.

Ziegler, G.M., Loos, A. (2017). “What is Mathematics?” and why we should ask, where one should experience and learn that, and how to teach it. In: Kaiser, G. (eds) Proceedings of the 13th International Congress on Mathematical Education. ICME-13 Monographs. Springer, Cham. https://doi.org/10.1007/978-3-319-62597-3_5

Download citation

DOI : https://doi.org/10.1007/978-3-319-62597-3_5

Published : 02 November 2017

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-62596-6

Online ISBN : 978-3-319-62597-3

eBook Packages : Education Education (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

• What is Mathematics?

4th ed. Jan 2024; 3rd ed. May 2023; 2nd ed. Dec 2009; 1st ed. Sep 2004

“It is not philosophy but active experience in mathematics itself that alone can answer the question: `What is Mathematics?'” – Richard Courant & Herbert Robbins, 1941, What is Mathematics?, Oxford University Press) “An adequate presentation of any science cannot consist of detailed information alone, however extensive. It must also provide a proper view of the essential nature of the science as a whole.” – Aleksandrov, 1956, Mathematics: Its Content, Methods, and Meaning

‘What is mathematics?’ Much ink has been spilled over this question, as can be seen from the selection of ten respected responses provided in the footnote 1 , with seven book-length answers, and three written in the current millenium. One might well ask, is there anything new that can be said, that should be said? We’ll start by clarifying what a good answer should look like, and then explore the answer proposed.

The rest of the paper follows the structure below:

1. Criteria for a ‘Satisfactory’ Definition of Mathematics

A satisfactory answer to the question ‘What is Mathematics?’ should, in my view, hold up well against the following three criteria:

Accordingly, it is not just ‘What is Mathematics today ?’ that we should be answering, but the broader scoped and more fundamental question: ‘Can we find a definition that adequately describes mathematics across the more than 5000 years of its written history ?’ In other words ‘Are there common threads that unite the practice of mathematics today with its long history and pre-history of mathematical practice ?’

The difficulty with the above criteria is that 1) our understanding of number, shape, and change stretches back into pre-history, 2) the concepts and applications that have emerged out of this understanding, what we may call mathematical practice, have seen profound evolution over the subsequent periods of mathematical history, in scope, in outlook, and in the organization of this mathematical knowledge, and 3) mathematicians today are investigating an enormous breadth of material, and the range of applications of mathematics is vast (to see this one need only glance at the subject classification of the American Mathematical Society , or the topics contained in the Princeton Companion to Pure Mathematics [Gowers, 2008] and Princeton Companion to Applied Mathematics [Higham, 2015]).

On the principle of requiring more than a current definition, we must therefore reject at the outset any definition of mathematics that is extracted from contemporary pure mathematics. Such definitions are often built around the abstract, deductive presentation of contemporary mathematics, organized axiomatically around a “sets with structure” theme. The problem with these definitions is that they would exclude vibrant, highly productive episodes in the history of mathematics up to the 19th century. They would exclude the pre-modern work of the Old Babylonians on pure mathematics within the scribal schools, the Neo-Babylonians on mathematical astronomy including a precursor of the differential calculus to interpolate the position of Jupiter, Omar Khayyam on the classification of the 19 classes of cubic equations and their complete solution using the intersection of at most two conics, and Fibonacci’s work. They would also exclude the work of Leibniz, Euler, the Bernoullis, Pascal on probability and combinatorics, Fermat on number theory, Lagrange, Laplace on the 3-body problem, and the work of other mathematicians, whose path-breaking advances were was NOT obtained axiomatically, coming after the adoption of symbolism in 1590 (Viete) but before the contemporary reformulation of mathematics axiomatically that began in the mid-1800s and accelerated in the mid-1900s. (For other limited answers also rejected, see Appendix 1.)

In what follows, we will attempt to build a definition of mathematics that covers earlier periods in the history of mathematics and also applies across the enormous range of pure and applied mathematics today. For the purpose of this article, we will consciously set aside additional, not inconsiderable, philosophical questions , such as ‘What is Truth?’, ‘What constitutes Proof?’, and ‘On what foundations does Mathematics build, and with what certainty?’ We’ll discuss a definition of Mathematics that is consistent with mathematical practice across its entire recorded history, from the first written account-keeping in Uruk by the Sumerians (c.3200 BCE), over the ensuing five millenia , to the present era with its its broad scope and modern practice in the present time.

We will proceed iteratively, in two passes. The first pass covers mathematics through to the end of the 18th century; the second pass extends the definition to cover mathematics through to the present.

2. First Pass: A definition covering all mathematics up end of the 18th century

“There are two fundamental sources of ‘bare facts’ for the mathematician, that is, there are some real things out there to which we can confront our understanding. These are, on the one hand the physical world which is the source of geometry, and on the other hand the arithmetic of numbers which is the source of number theory. Any theory concerning either of these subjects can be tested by performing experiments either in the physical world or with numbers.” – Alain Connes (mathematician, Fields Medalist 1982) from Non-Commutative Geometry, 2000

Definition 1: Mathematics is a subject concerned with number, shape, and change.

These first three elements adequately cover pre-modern mathematics and modern mathematics upto the end of the 18th century including the mathematics of ancient Babylonia, Egypt, Greece 2 , China, India, Arabia and Central Asia 3 This includes numeration systems, integer arithmetic, division of property, taxation, and arithmetic of fractions, Euclidean geometry and its offshoots astronomy and trigonometry, solution of algebraic equations lower than degree five, mensuration, the properties of various two and three dimensional figures, the fundamentals of statics and mechanics, dynamics, infinite series, and even the differential and integral calculus, and physics. In particular, this definition covers the works of Euler, Laplace, Taylor, Newton, etc. Most importantly, the mathematics up to the start of the 19th century, was about the real, physical world, and was a language used to investigate its notions. Mathematics for a long time had been considered either part of accounting, a part of geometry, or a branch of natural philosophy. The mathematics up to the end of the 18th century was concerned with the “bare facts” of this physical and arithmetically coherent world:

To cover contemporary mathematics from the 19th century onward requires further elements, the notion of mathematical structure and the study of relations between mathematical objects and mathematical structures. It requires a deeper understanding of how mathematics has and continues to develop.

Let’s start with the word itself. “ Matema” is the ancient Greek term for “that which is learnt,” or “what one gets to know.” So we get the first pillar: Mathematics is a body of knowledge, and area of human understanding. But knowledge and understanding of what?

There are two compelling perspectives: the dialetic perspective of the philosopher-mathematican Imre Lakatos and the anthropology of mathematics perspective of mathematical historian Jens Hoyrup.

3. Mathematics as dialectic and an Anthropology of Mathematics

“In the history of the development of mathematics, three different processes of growth now change places, now run side by side independent of one another, now finally mingle. Plan A is based upon a more particularistic conception of science which divides the total field into a series of mutually separated parts and attempts to develop each part for itself, with a minimum of resources and with all possible avoidance of borrowing from neighboring fields. Its idea is to crystallize out each of the partial fields into a logically closed system. Plan B lays the chief stress upon the organic combination of the partial fields, and upon the stimulation which these exert one upon another. Plan B prefers, therefore, the methods which open an understanding of several fields under a uniform point of point of view. Its ideal is the comprehension of the sum total of mathematical science as a great connected whole. There is still a third Plan C, algorithmic, which, along side of and within the processes of development A and B, often plays an important role as a quasi-independent, onward-driving force, inherent in the formulas, operating apart from the intention and insight of the mathematician, at the time , often indeed in opposition to them.” – Felix Klein, 1908, Elementary Mathematics from an Advanced Perspective, pp.77-85

1. Mathematics as dialectic . In this perspective, mathematics is a great conversation, happening through time, and across traditions, a conversation about ideas, refining, reworking, testing and objecting, ultimately uncovering new and deeper understanding. This is the perspective of [Lakatos, 1976, Proofs and Refutations] and of [Aleksandrov, 1956, A General View of Mathematics]. Lakatos illustrates this with a facinating dialogue between a group of students debating the proof of the Euler characteristic of the polyhedron, artfully compressing into a single dialogue understanding that evolved over the course of approx. 200 years. Aleksandrov focuses on the results of the dialectic, on the steady progress of mathematical concepts: “they are brought into being by a series of successive abstractions and generalizations, each resting on a combination of experience with preceding abstract concepts.[Aleksandrov, 1956, p.17]

There is another aspect of dialectic, a dialectic tension of ideas, concepts, and perspectives, which Felix Klein brings out clearly in the quote displayed at the start of this section [Klein, 1908, 77-85].

In it, Klein describes how in the history of mathematics, the interplay between these three Plans for mathematics moved back and forth, unifying, specializing, unifying again. What drove the impulses between them are both impulses within the individual mathematician and anthropological (social and culture) influences, mainly from the requirement to teach comprehensibly, which ties to a second important perspective.

For an equally fascinating didactic exploration of the nature of mathematics, one is recommended to read Renyi’s “Dialogues on Mathematics” [Renyi, 1967], in which a Socrates discusses the nature of mathematics, an Archimedes discusses the applications of mathematics, and Galileo discusses the ability of mathematics to assist in uncovering the workings of nature. (The first of these 3 dialogues is reproduced in [Hersh, 2006, Ch.1]).

2. The anthropology of mathematics takes the perspective that “the character of mathematical thinking and argument is strongly affected — indeed is almost essentially determined — by the dynamics of the specific social, mostly professional environments in which it is carried” [Hoyrup, 2017], i.e. mathematics is shaped by the interplay between the characteristics of a society and, in particular, the institutions for teaching which influence mathematical thought, research directions, and determine the limits of mathematical practice. The term “anthropology of mathematics” 4 is due to Jens Hoyrup [Hoyrup, 1980, 1994, 2017, 2019] with the catalyzing idea coming from a paper by Judith Grabiner [Grabiner, 1974]. Grabiner showed how the rise of university teaching of mathematics in France and Germany in the 1800s created pressure to make the mathematics of Newton, Leibniz, Euler, and the Bernoullis more easily accessible to students, which in turn accelerated the re-emergence of deductive mathematics. Taking this as a launching point, Jens Hoyrup in ground-breaking researches from 1980 onward, meticulously investigated and detailed the same phenomenon in the major pre-modern mathematical centres (Babylonia, Greece, Islamic Spain to Afghanistan, and mercantile Italy). Hoyrup showed [Hoyrup, 1994] how the temple culture in the early city-states of Sumeria and the rise of scribal schools shaped mathematical development over the entire Sumero-Akkadian-Old Babylonian period (3200-1600 BCE). He shows how in ancient Greece the decentralization of teaching ( sophists were the early itinerant teachers) and the philosophical pre-occupation of aristocratic Greek society, shaped the lens through which the Greeks approached the corpus of 2000 years of Babylonian and Egyptian mathematics and created a new, philosophical, deductive science. [Hoyrup, 2019] With the exception of the Greek experience, a sort of practitioner’s, or utilitarian mathematics (what Hoyrup calls subscientific mathematics ).

Perhaps the strongest case for the anthropology of mathematics (culture as a carrier and the socially specific institutions of teaching) is the fact that the uniquely Greek creation of a deductive reasoning did not persist beyond Alexandria, neither in the era of mathematics in the Islamic period, nor in the pre-Renaissance Abacus period, both of which were dominated by the subscientific, practitioner approach to mathematics which also under-pinned both Babylonian and Egyptian mathematics. [Hoyrup, 1990, 1994, 2003].

Hoyrup’s researches since 1980 have shown that: “Old Babylonian ‘algebra’ and Euclidean ‘geometric algebra’ were connected. The geometric riddles of Arabic misaha treatises as well as al-Khwarizmi’s geometric proofs for the basic al-jabr (algebra) procedures belonged within the same network. The Old Babylonian ‘algebraic’ school discipline built upon original borrowings from the ‘neck riddles’ of a lay surveyor’s environment, and that this environment and its riddles, not the tradition of scholar-scribes, was responsible for the transmission of the inspiration to later times [both to the Greeks as well as to the Islamic scientists].” [Hoyrup, 2003, 9] He points out that there is a continuity of problem classes all the way through to the 1200s CE in Jacopo’s Algebra, and Fibonacci (Leonardo of Pisa)’s Liber Abaci. “These belong to a cluster of problems that are found in ancient and medieval sources from Ireland to India. This cluster of problems that usually go together was apparently carried by the community of merchants travelling along the Silk Road and adopted as ‘recreational problems’ by the literate in many places; it is thus a good example of a body of sub-scientific knowledge influencing school knowledge in many places and an illustration of the principle that it is impossible to trace the ‘source’ for a particular trick or problem in a situation where ‘the ground was wet everywhere’.

Hoyrup’s anthropology of mathematics perspective also addresses the WHEN aspect of mathematics:

[We may say that] transition[s] to [M]athematics occurred [in history] when pre-existent and previously independent mathematical practices and techniques were wielded by specialist practitioners who were organized professionally and linked in a network of communication. Such professional groups fall into two main types: in one type knowledge is transmitted within an apprenticeship-system of ‘learning by doing under supervision’ [sub-scientific mathematics]. The other type involves some kind of school [in which] teaching is separate from actual work. In the former type, those who transmit are actively involved in the practical activities of their trade; they will tend to train exactly what is needed, and the understanding they will try to communicate will be that of practical procedures. [In the latter type, the] school teaching of mathematical skill is bound to a writing system extensive enough to carry a literate culture. [While] teachers in the school type may well have as their aim to impart knowledge for practice, the mathematical understanding that they teach will concentrate on inner connections of the topic, i.e. on mathematical explanations.” – Jens Hoyrup, 2017, Perspectives on an Anthropology of Mathematics

Subscientific mathematical culture and pre-modern rhetorical mathematical practice does not mean that the mathematics was primitive, nor that there was no pure mathematics. “On the contrary, at various points in its history, in particular during the Old Babylonian period, mathematical activity turned toward the pure and systematic, pursued for supra-utilitarian reasons, what we might call scientific, or perhaps better systematic.” [Hoyrup, 1980]. In the past 40 years, examples have been discovered of creative and advanced approaches, including a pre-cursor of our Calculus already being used by the Neo-Babylonians of c.500 BCE to predict the position of Jupiter in the night-sky .

Creative progress in European mathematics before the Renaissance (pre-1300s) was constrained by Aristotelian philosophy on the one hand, Euclidean geometry on the other, and the monastic preservation of classical knowledge as a received but not an indiginous intellectual activity. Even when this influenced finally lifted with the rise of the Abacus schools in Italy (1300s-1400s), and when mathematical practice shifted away from rhetorical to symbolic around Francois Viete (1591) who began the extensive use of symbols in calculation, even then the form of mathematical creative culture was not deductive, even if the results were presented that way (see e.g. Newton’s Principia). Only from the mid-1800s did creative mathematical advancement occur again in the deductive style of the classical Greece, this time in the axiomatic works of Boole (logic), Cayley, Weber, Dedekind, Noether (abstract algebra), Cauchy, Bolzano, Weierstrass, Dedekind, Cantor (analysis), culminating in the the formalist program of Hilbert and the structuralist organization of all of mathematics from the 1950s.

We see the similar effects of culture on contemporary mathematics (New Math in the 1960s and its pushback and subsequent splintering of approaches in the 2000s).

But while the dialectic perspective and the anthropology of mathematics perspective do not tell us WHAT this great conversation is about, they do tell us a lot about HOW it happens. And that HOW provides the missing fifth element to complete our definition.

We now have what we need to answer directly:

4. Second Pass: A definition covering all mathematics, including contemporary mathematics

Definition 2: Mathematics is a body of knowledge, built up over time in a dialetic process, on matters whose origin lies in the three natural phenomena: quantity (number, measurement, scale), space (shape, configuration, arrangement, symmetry, perspective), transformation (change, variation), shaped by the prevailing social culture, and in turn influencing it (often profoundly) through its diverse, and often ingenious, applications.

Deepening understanding of the three natural phenomena lead to the development of a chain of evolving conceptual abstractions, to greater generalization, and to correspondingly broader areas of investigation. Observation of relations (association, comparison, similarity, equivalence) between diverse mathematical phenomenona has created a fifth, humanistic area of mathematical activity: the rational structuring of its accumulated body knowledge through the development of axiomatic (deductively structured) mathematical systems that generalize and extend empirical concepts, introduce fundamentally new theoretical concepts, and examine the laws that govern their structure, properties, and the relationships between them.

Let’s look in turn at the elements.

The first three are elaborated versions of what we had before:

The fifth element brings it all together:

Also worth a further comment is the remark on the influence of mathematics on society through applications. I rather hope that this statement is not controversial. The applications of mathematics are everywhere, amplified through science and engineering. To take but one example, the development of operations research to optimize military supply chains and bombing patterns against U-boats in WWII.

5. Testing the expanded definition against contemporary mathematical practice

We have seen how the first three elements were sufficient to cover mathematics up to the start of the 19th century.

The last two elements (relation and structure) are INTROSPECTIVE views. They are about mathematicians looking at the mathematics that they know and asking how/why they know it and how best to capture/catalogue that knowledge. With the addition of “structure”, we cover the axiomatic mathematics that returned again to the 19th century universities in France and Germany. We are able to cover the development of abstraction in the notions of algebra and number and an abstract algebraic mathematical logic in the early part of the 1800s, led by the English mathematicians George Peacock, George Boole, Augustus De Morgan, and then William Rowan Hamilton, Cayley, and then picked up in Germany by Weber, Noether, Klein, Lie, and others developing abstract algebra, and discovering its power to unlock additional questions.

We are also able to cover the transition from the intuitive mathematics of the 18th-century to the formalist mathematics of the 19th- and 20th-centuries, including the development of set theory as the foundation of the real numbers and analysis (Cauchy, Weierstrass, Dedekind), and the higher cardinalities (Cantor), the rise of point-set topology, functional analysis, linear algebra (geometry in n dimensions), measure theory and the axiomatic foundations of probability (Kolmogorov), and much more.

Is the Fifth Element really new? What is fascinating in this story is that when one takes Hoyrup’s viewpoint of “anthropology of mathematics”, then this fifth element, introspection on its content, has been with mathematics throughout its known/recorded history, influencing how knowledge is organized, arranged, simplified, rigorized. Hoyrup’s research shows that it appears in every culture and context through the pre-modern mathematical period. It appears differently depending on the social and institutional context of the time (this is the anthropological perspective), but it appears nonetheless. So it is not the case that the current modern axiomatic style is somehow a natural endpoint in a linear mathematical development. On the contrary, there have been periods of more or less rigour, more or less scientific vs. subscientific (utilitarian) styles. Indeed the two high points of the rigorous axiomatic approach have been the Greek period 500 BCE-200 BCE and from the 19th-century onward. Both have seen the primacy of developing logically structured (axiomatic) mathematical systems that systematize, generalize and extend empirical concepts.

Why is this important? Because it is introspection, the fifth element, I claim, that gives mathematics its essential restlessness, its continual development, resifting, refinement of mathematical knowledge, and the exploration of other subjects using a mathematical lens. It has always been the source of advancement in every age of mathematics, and this continues in contemporary mathematics. Because it is the element that introduces new theoretical concepts, and simplifies and clarifies existing concepts by examining the laws that govern their structure, finding deep structural analogies between superficially dissimilar context.

The systematization of mathematics as a science has inevitably led to deeper understanding of the three natural phenomena. The breadth of modern mathematics is organized within these mathematical systems, and it is from within these systems that they find application in areas beyond the historical core. Where conceptual abstractions have evolved, and effective generalizations have been found, these have in turn led to correspondingly broader areas of investigation. For example, modern mathematical physics (gauge theories, string theories, quantum field theories), has advanced materially through the contributions of abstract algebra, continuous group theory, and the theory of representations. So also have several other fields, for example computer science (computability, recursion, mathematical linguistics), biology (chaos theory, self-organizing systems), economics, finance , linguistics and fuzzy logic , and others.

6. A Deeper Look: Three Facets of Mathematics

To properly understand Mathematics in a way that is consistent with its history, evolution, and its many diverse applications, as well as with its contemporary, abstract, and highly specialized state, we need to go beyond the definition. Here it is helpful to identify three co-existing facets of Mathematics:

These facets of Mathematics explain both the historical development, maturity, and modern separation between theoretical and applied considerations. Let’s look at each in turn.

6.1. Mathematics as an Empirical Science  

Mathematics originates out of science, i.e. out of human interest in the surrounding world, its careful observation, and the empirical verification of mathematical fact. In fact, the world and its patterns are consistently present in the inspiration of all mathematical studies. Even the abstract, abstruse, and seemingly detached topics of advanced higher mathematics are generalizations of patterns observed in the layers of less abstract mathematics, that are themselves an attempt to capture patterns observed in the real world itself.

Thus, the essence of a mathematical concept can always be related back to an original proto-concept that has its roots in empirical observations and the patterns arising out of these.

6.2. Mathematics as a Modeling Art  

Mathematics as a modeling art involves an effort to develop, maintain, and perfect models of perceived or envisioned reality. Mathematics has always involved, and continues to involve, the exploration, explanation and modeling of phenomena.

At the root of this facet of mathematics is the intimate relationship between the physical world and the world of mathematical ideas. Most of the major laws of mathematics are modeled on actual physical occurrences, suitably abstracted. Thus, the origin of most of mathematics is a model of something real that has been experienced. Indeed, typical applied mathematics proceeds from a physical context to the context of a mathematical model, performs computations and analysis using mathematical reasoning within the domain of this model, and then finally brings the result back to the physical context for interpretation.

The success of Mathematics in keeping ever-improving mathematical models of many and various phenomena, and the fact that the methods behind these models are often applicable in widely different areas and contexts, often lead Mathematics to be viewed enthusiastically (though incorrectly) as the key to the knowledge of all things. 5

6.3. Mathematics as an Axiomatic Arrangement of Knowledge  

The exploration of the logical structure of mathematical knowledge is a relatively recent development, beginning with the ancient Greeks circa 800 BCE. Comparatively, this phenomenon has occupied less than 3 millenia, or less than 10% of the documented history of mathematical knowledge of humankind (30,000 years).

Rapid progress in understanding the logical structure of mathematics occurred since the 1800s CE,and has led to the flowering of a wide variety of modern mathematical systems and theories whose areas of interests and domains of application go far beyond the historical core of mathematics. To put it in context, the past 200 years of mathematics since 1800 CE is less than 5% of the documented history of mathematics.

Today, the vast scope of modern mathematical knowledge is organized within structured mathematical systems from within which it finds wide application.

Mathematical structures distill informal mathematical knowledge, identify the important concepts out of the body of informal mathematical knowledge, and provide streamlined logical models to underpin these areas.

7. Mathematics “from the inside”

I will close with a few observations of mathematics ‘from the inside’, i.e. mathematicians writing about mathematics :

“Mathematics is the backbone of modern science and a remarkably efficient source of new concepts and tools to understand the ‘reality’ in which we participate. The new concepts themselves are the result of a long process of ‘distillation’ in the alembic 6 of human thought.” – Alain Connes, (mathematician, Fields Medalist 1982), from Advice to the Beginner, 2006

The interplay between generality and individuality, deduction and construction, logic and imagination—this is the profound essence of live mathematics. Any one or another of these aspects of mathematics can be at the center of a given achievement. In a far reaching development all of them will be involved. Generally speaking, such a development will start from the “concrete” ground, then discard ballast by abstraction and rise to the lofty layers of thin air where navigation and observation are easy; after this flight comes the crucial test of landing and reaching specific goals in the newly surveyed low plains of individual “reality”. In brief, the flight into abstract generality must start from and return again to the concrete and specific. — Richard Courant (mathematician), from Mathematics in the Modern World, Scientific American Vol.211 No.3, pp.41-49, 1964

One cannot escape the feeling that these mathematical formulae have an independent existence and an intelligence of their own, that they are wiser than we are, wiser even than their discoverers, that we get more out of them than we originally put into them. — Heinrich Hertz (physicist), from Men of Mathematics, Vol 2, p.16, 1937

Very often in mathematics the crucial problem is to recognize and to discover what are the relevant concepts; once this is accomplished the job may be more than half done. — I.N. Herstein (mathematician), Topics in Algebra

It looked absolutely impossible. But it so happens that you go on worrying away at a problem in science and it seems to get tired, and lies down and lets you catch it. — William Lawrence Bragg \footnote{Bragg, at age 24, won the Nobel Prize for the invention of x-ray crystallography. He remains the youngest person ever to receive the Nobel Prize.}

(For more quotes on Mathematics and the process of doing mathematics , see here.)

8. Continue Reading

Appendix 1: answers deemed unsatisfactory to the criteria outlined above.

Several authors attempt to answer the title question by providing a survey of mathematics but this in my view is as unhelpful as stating that ‘mathematics is the sum of its contents’. An author should not have to take an intelligent reader through 300+ pages of technical material before providing an clear answer. The caveat of course is that that one must have actively experienced enough mathematics (and for our purposes, enough exposure to its history) to find the answer satisfying.

A second frequently given, but also limiting answer, is that mathematics is the exploration through deductive reasoning of mathematical structures whose properties are abstracted into axioms from objects of practical experience. Simplified, this boils down to mathematics as the study of necessary deductions, which is problematic. It covers much of contemporary mathematics which is built around abstraction and deduction and organized into areas defined by the structures they study (groups, rings, fields, lattices, manifolds, functions, sets, logic structural presentation of contemporary mathematics). While it roots mathematics in practical experience, it denies that there can be mathematics that is not deductive, which is problematic given the long periods of history (before classical Greece and between classical Greece and the 1800s) when much mathematical knowledge was discovered without the use of a formal deductive style of arrangement of that knowledge. [See Hoyrup, 1980, 1994, 2019] To use a metaphor, if the deductive structure of mathematics is like varnish on wood, then we cannot accept that it is only the varnished variety of wood that is mathematics, but not the wood itself. The appeal of varnished wood is aesthetic, its longevity perhaps more assured, but the essential element is the wood, much of which is not easy to discover (as anyone who has tried will find). Hoyrup identifies the separate traditions as “scientific” and “sub-scientific”. Of the sub-scientific tradition, it is rooted in problem-solving and historically persisted even when the scientific tradition waned, as it did after Old Babylonian high point and after classical Greece. (Hoyrup, 1980, 1994, 2001), (Grabiner, 1976). In our view, both are entitled to be called mathematics.

9. References

Group 2: Expository content that supports the views expressed in this article

Group 3: Surveys of Mathematics

Group 4: Additional Recommended Reading

• Responses from 1941 to 2017: (Courant, Robbins, 1941), (Alexandrov, Kolmogorov, Lavrentiv, 1963), (Renyi, 1967), (Halmos, 1973), (Lakatos, 1976), (Davis, Hersh, 1981), (MacLane, 1986), (Hersh, 2006), (Zeilberger, 2017), (Hoyrup, 2017), 7 books, 3 articles. ↩
• The Greeks had already encountered the paradoxes of the real numbers, though not their resolution, and were already using the method of exhaustion and converging upper and lower bounds, a precursor to the methods of the integral calculus, apart from a rigorous passing to the limit. ↩
• The Arab and Central Asians and Indians advanced algebra to an abstract science, had resolved the solution of algebraic equations including most instances of the general cubic, had developed expansion by Taylor series and precursors of the calculus, had developed the trigonometric identities, applied algebra and trigonometry to astronomical problems, and had fully developed systems of computation for interest rates, taxation, and other numerical calculations using decimal digits including zero, and a place decimal system. ↩
• “(paraphrased) The actual content of mathematics, the changing mode of mathematical thought, the functions mathematics can fulfill, and the pursuit and development of mathematics (are) conditioned by the wider social and cultural context.” “Individual contributors are seen as members of one or perhaps several intersecting subgroups within a general cultural matrix.” “The character and substance of scientific thinking and the aims pursued by the sciences, as well as insitutions, ideologies, and general social need, change when mathematical development is considered over longer periods or when comparing between different cultures, which requires dialectical synthesis.” The content of mathematics (and) its interaction with the sociocultural setting (Hoyrup, 1994, p.xii-xiii). ↩

“a thorough study of all things, insight into all that exists, knowledge of all obscure secrets.” ( Bur , p.38.)

• an “alembic” is an obsolete apparatus used by alchemists for the distillation of liquids – it’s a suggestive metaphor. ↩

3 comments to What is Mathematics?

Thanks, I was interested in your perspective about what mathematics is and the nature of mathematics.

I saw this really good post today.

[…] to strengthen the understanding of technically important developments in a way that is memorable, i.e. that can be understood fully and reproduced at will. (For the first three objectives, see What is Mathematics?) […]

Leave a Reply

You can use these HTML tags

<a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

   Name (required)

   Email (will not be published) (required)

   Website

Save my name, email, and website in this browser for the next time I comment.

Your comments are valued! (Please indulge the gatekeeping question as spam-bots cannot (yet) do simple arithmetic...) - required In order to pass the CAPTCHA please enable JavaScript

Upload attachment   (Allowed file types: jpg, gif, png, pdf, doc, docx, ppt, pptx, xls, xlsx, avi , maximum file size: 6MB.

Optionally add an image (JPEG only)

  Notify me when new comments are added to this post.

Stats : 1,089,379 article views since 2010 (Aug '24 update)

Dear Readers:

Welcome to the conversation!  We publish long-form pieces as well as a curated collection of spotlighted articles covering a broader range of topics.   Notifications for new long-form articles are through the feeds (you can join below).  We love hearing from you.  Feel free to leave your thoughts in comments, or use the contact information to reach us!

Reading List…

Looking for the best long-form articles on this site? Below is a curated list by the main topics covered.

Mathematics History & Philosophy

• Prehistoric Origins of Mathematics
• The Mathematics of Uruk & Susa (3500-3000 BCE)
• How Algebra Became Abstract: George Peacock & the Birth of Modern Algebra (England, 1830)
• The Rise of Mathematical Logic: from Laws of Thoughts to Foundations for Mathematics
• Mathematical Finance and The Rise of the Modern Financial Marketplace
• A Course in the Philosophy and Foundations of Mathematics
• The Development of Mathematics
• Catalysts in the Development of Mathematics
• Characteristics of Modern Mathematics

Topics in Mathematics: Pure & Applied Mathematics

• Fuzzy Classifiers & Quantile Statistics Techniques in Continuous Data Monitoring
• LOGIC in a Nutshell: Theory & Applications (including a FORTH simulator and digital circuit design)
• Finite Summation of Integer Powers: ( Part 1 | Part 2 | Part 3 )
• The Mathematics of Duelling
• A Radar Tracking Approach to Data Mining
• Analysis of Visitor Statistics: Data Mining in-the-Small
• Why Zero Raised to the Zero Power IS One

Technology: Electronics & Embedded Computing

• Electronics in the Junior School - Gateway to Technology
• Coding for Pre-Schoolers - A Turtle Logo in Forth
• Experimenting with Microcontrollers - an Arduino development kit for under £12
• Making Sensors Talk for under £5, and Voice Controlled Hardware
• Forth, Lisp, & Ruby: languages that make it easy to write your own domain specific language (DSL)
• Programming Microcontrollers: Low Power, Small Footprints & Fast Prototypes
• Building a 13-key pure analog electronic piano.
• TinyPhoto: Embedded Graphics and Low-Fat Computing
• Computing / Software Toolkits
• Assembly Language programming ( Part 1 | Part 2 | Part 3 )
• Bare Bones Programming: The C Language

Technology: Sensors & Intelligent Systems

• Knowledge Engineering & the Emerging Technologies of the Next Decade
• Sensors and Systems
• Unmanned Autonomous Systems & Networks of Sensors
• The Advance of Marine Micro-ROVs

Maths Education

• Maxima: A Computer Algebra System for Advanced Mathematics & Physics
• Teaching Enriched Mathematics, Part 1
• Teaching Enriched Mathematics, Part 2: Levelling Student Success Factors
• Logic, Proof, and Professional Communication: five reflections
• Good mathematical technique and the case for mathematical insight

Browse…

Explore….

• Math Article
• What is Mathematics

What is Mathematics?

Mathematics is one of the most important subjects. Mathematics is a subject of numbers, shapes, data, measurements and also logical activities. It has a huge scope in every field of our life, such as medicine, engineering, finance, natural science, economics, etc. We are all surrounded by a mathematical world.

The concepts, theories and formulas that we learn in Maths books have huge applications in real-life. To find the solutions for various problems we need to learn the formulas and concepts. Therefore, it is important to learn this subject to understand its various applications and significance.

What Is The Definition of Mathematics?

Mathematics simply means to learn or to study or gain knowledge. The theories and concepts given in mathematics help us understand and solve various types of problems in academic as well as in real life situations.

Mathematics is a subject of logic. Learning mathematics will help students to grow their problem-solving and logical reasoning skills. Solving mathematical problems is one of the best brain exercises.

Basic Mathematics

The fundamentals of mathematics begin with arithmetic operations such as addition, subtraction, multiplication and division. These are the basics that every student learns in their elementary school. Here is a brief of these operations.

• Addition: Sum of numbers (Eg. 1 + 2 = 3)
• Subtraction: Difference between two or more numbers (Eg. 5 – 4 = 1)
• Multiplication: Product of two or more numbers (Eg. 3 x 9 = 27)
• Division: Dividing a number into equal parts (Eg. 10 ÷ 2 = 5, 10 is divided in 2 equal parts)

History of Mathematics

Mathematics is a historical subject. It has been explored by various mathematicians across the world since centuries, in different civilizations. Archimedes, from the BC century is known to be the Father of Mathematics. He introduced formulas to calculate surface area and volume of solids. Whereas, Aryabhatt, born in 476 CE, is known as the Father of Indian Mathematics.

In the 6th century BC, the study of mathematics began with the Pythagoreans, as a “demonstrative discipline”. The word mathematics originated from the Greek word “mathema”, which means “subject of instruction”.

Another mathematician, named Euclid, introduced the axiom, postulates, theorems and proofs, which are also used in today’s mathematics.

History of Mathematics has been an ancient study and is described by each part of the world, in a varying method. There were many mathematicians who have given different theories for many concepts, which we are applying in modern mathematics.

Numbers, which we use for calculations, had variations in the medieval period. The Romans introduced the Roman numerals that uses English alphabets to represent a number, such as:

Branches of Mathematics

The main branches of mathematics are:

• Number System
• Trigonometry
• Probability and Statistics

These mathematical concepts fall under pure mathematics . These form the base of mathematics. In our academics we will come across all these theories and fundamentals to solve questions based on them.

Applied mathematics is another form, where mathematicians, scientists or technicians use mathematical concepts to solve practical problems. It describes the professional use of mathematics.

Symbols in Mathematics

Some of the basic and most important symbols, used in mathematics, are listed below in the table.

These are the most common symbols used in basic mathematical calculations. To get more maths symbols click here.

Properties in Mathematics

In mathematics, we learn about four major properties of numbers. They are:

• Commutative Property
• Associative property
• Distributive Property
• Identity Property

These are the four basic properties of numbers. These properties are also applicable to some other mathematical concepts such as algebra.

Rules in Mathematics

The most common rule used in mathematics is the BODMAS rule. As per this rule, the arithmetic operations are performed based on the brackets and order of operations. By the full form of BODMAS, we can easily understand this logic.

BODMAS – Brackets Orders Division Multiplication Addition and Subtraction

Therefore, the first priority here is given to the brackets then division>multiplication>addition>subtraction.

For example, if we have to solve [5+(3 x 5)÷2], then using the BODMAS rule, first multiply 3 and 5, within the brackets.

→ 5+(3 x 5)÷2 = 5 + 15÷2

Now divide 15 by 2

Formulas in Mathematics

Here are some common formulas used in mathematics to solve multiple problems.

• Area and Perimeter Formula
• Coordinate Geometry Formulas
• Heron’s Formula
• Quadratic Formula
• Differentiation Formulas
• Distance Formula
• Section Formula & Conic Sections
• Standard Deviation Formula
• Trigonometry Formulas

Topics in Mathematics

Let us see some important topics for each Class (from 1 to 12) that are covered under mathematics.

Class 1 Mathematics

• Numbers In Words
• Addition And Subtraction Of Integers

Class 2 Mathematics

• Counting Numbers
• Place Value

Class 3 Mathematics

• Multiplication Tables
• Multiplication And Division Of Integers
• Comparing Fractions
• Introduction To Data

Class 4 Mathematics

• Factors And Multiples
• Multiplication And Division Of Decimals
• Multiplying Fractions
• Introduction to Large Numbers

Class 5 Mathematics

• Dividing Fractions
• Addition and Subtraction of Decimals
• Lines and Angles Introduction
• Area Of A Square – Introduction To Area

Class 6 Mathematics

• Whole Numbers

Class 7 Mathematics

• Lines And Angles
• Percentage: Means Of Comparing Quantities
• Visualising Solid Shapes

Class 8 Mathematics

• Rational Numbers
• Mensuration
• Squares and Square Roots
• Exponents And Powers

Class 9 Mathematics

• Polynomials
• Quadrilateral
• Surface Areas and Volume

Class 10 Mathematics

• Arithmetic Progression
• Co-ordinate Geometry
• Constructions
• Probability And Statistics

Class 11 Mathematics

• Relations and Functions
• Trigonometric Functions
• Linear Inequalities
• Permutation And Combination
• Conic Sections
• Limits and Derivatives

Class 12 Mathematics

• Inverse Trigonometric Functions
• Determinants
• Application of Integrals
• Vector algebra
• Linear Programming
• Continuity And Differentiability

Frequently Asked Questions on Mathematics

Define mathematics..

Mathematics is a subject that deals with numbers, shapes, logic, quantity and arrangements. Mathematics teaches to solve problems based on numerical calculations and find the solutions.

Why is Mathematics an important subject for students?

Learning mathematics will help students to build their logical thinking and problem solving skills. It has huge applications in day to day life. The basic arithmetic operations such as addition, subtraction, multiplication and division are the most important part of our lives. Based on these operations, we do numerous calculations.

Who is the Father of Mathematics?

Archimedes, (287-212 BC) is known to be the Father of Mathematics.

Which part of mathematics does Trigonometry belong to?

Geometry is one of the most important branches of mathematics that includes trigonometry, where we deal with sides and angles of a right triangle. It has huge applications in the fields of construction and architecture.

What are the two forms of Mathematics?

Mathematics is described in two forms:

Pure mathematics and Applied mathematics

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

What is mathematics?

Mathematics is at the heart of science and our daily lives.

• Inventor of mathematics
• Ancient Greek Mathematics
• Importance of mathematics

Mathematics is the science that deals with the logic of shape, quantity and arrangement. Math is all around us, in everything we do. It is the building block for everything in our daily lives, including mobile devices, computers, software, architecture (ancient and modern), art, money, engineering and even sports.

Since the beginning of recorded history, mathematical discovery has been at the forefront of every civilized society, and math has been used by even the most primitive and earliest cultures . The need for math arose because of the increasingly complex demands from societies around the world, which required more advanced mathematical solutions, as outlined by mathematician Raymond L. Wilder in his book " Evolution of Mathematical Concepts " (Dover Publications, 2013). 

The more complex a society, the more complex the mathematical needs. Primitive tribes needed little more than the ability to count, but also used math to calculate the position of the sun and the physics of hunting. "All the records — anthropological and historical — show that counting and, ultimately, numeral systems as a device for counting form the inception of the mathematical element in all cultures," Wilder wrote in 1968.

Who invented mathematics?

Several civilizations — in China , India, Egypt , Central America and Mesopotamia — contributed to mathematics as we know it today. The Sumerians, who lived in the region that is now southern Iraq, were the first people to develop a counting system with a base 60 system, according to Wilder. 

This was based on using the bones in the fingers to count and then use as sets, according to Georges Ifrah in his book " The Universal History Of Numbers " (John Wiley & Sons, 2000). From these systems we have the basis of arithmetic, which includes basic operations of addition, multiplication, division, fractions and square roots. Wilder explained that the Sumerians' system passed through the Akkadian Empire to the Babylonians around 300 B.C. Six hundred years later, in Central America, the Maya developed elaborate calendar systems and were skilled astronomers. About this time, the concept of zero was developed in India.

As civilizations developed, mathematicians began to work with geometry, which computes areas, volumes and angles, and has many practical applications. Geometry is used in everything from home construction to fashion and interior design. As Richard J. Gillings wrote in his book " Mathematics in the Time of the Pharaohs " (Dover Publications, 1982), the pyramids of Giza in Egypt are stunning examples of ancient civilizations' advanced use of geometry.

Geometry went hand in hand with algebra . Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī authored the earliest recorded work on algebra called "The Compendious Book on Calculation by Completion and Balancing" around 820 A.D., according to Philip K. Hitti , a history professor at Princeton and Harvard University. Al-Khwārizmī also developed quick methods for multiplying and dividing numbers, which are known as algorithms — a corruption of his name, which in Latin was translated to Algorithmi.

Algebra offered civilizations a way to divide inheritances and allocate resources. The study of algebra meant mathematicians could solve linear equations and systems, as well as quadratics , and delve into positive and negative solutions. Mathematicians in ancient times also began to look at number theory, which "deals with properties of the whole numbers, 1, 2, 3, 4, 5, …," Tom M. Apostol, a professor at the California Institute of Technology, wrote in " Introduction to Analytic Number Theory " (Springer, 1976). With origins in the construction of shape, number theory looks at figurate numbers, the characterization of numbers, and theorems.

Mathematics in ancient Greece

The word mathematics comes from the ancient Greeks and is derived from the word máthēma, meaning "that which is learnt," according to Douglas R. Harper, author of the " Online Etymology Dictionary ." The ancient Greeks built on other ancient civilizations’ mathematical studies, and they developed the model of abstract mathematics through geometry. 

Greek mathematicians were divided into several schools, as outlined by G. Donald Allen, professor of Mathematics at Texas A&M University in his paper, " The Origins of Greek Mathematics ":

In addition to the Greek mathematicians listed above, a number of other ancient Greeks made an indelible mark on the history of mathematics, including Archimedes , most famous for the Archimedes' principle around the buoyant force; Apollonius, who did important work with parabolas ; Diophantus, the first Greek mathematician to recognize fractions as numbers; Pappus, known for his hexagon theorem; and Euclid, who first described the golden ratio .

During this time, mathematicians began working with trigonometry , which studies relationships between the sides and angles of triangles and computes trigonometric functions, including sine, cosine, tangent and their reciprocals. Trigonometry relies on the synthetic geometry developed by Greek mathematicians like Euclid. In past cultures, trigonometry was applied to astronomy and the computation of angles in the celestial sphere.

The development of mathematics was taken on by the Islamic empires, then concurrently in Europe and China, according to Wilder. Leonardo Fibonacci was a medieval European mathematician and was famous for his theories on arithmetic, algebra and geometry. The Renaissance led to advances that included decimal fractions, logarithms and projective geometry. Number theory was greatly expanded upon, and theories like probability and analytic geometry ushered in a new age of mathematics, with calculus at the forefront.

Development of calculus

In the 17th century, Isaac Newton in England and Gottfried Leibniz in Germany independently developed the foundations for calculus, Carl B. Boyer, a science historian, explained in " The History of the Calculus and Its Conceptual Development " (Dover Publications, 1959). Calculus development went through three periods: anticipation, development and rigorization. 

In the anticipation stage, mathematicians attempted to use techniques that involved infinite processes to find areas under curves or maximize certain qualities. In the development stage, Newton and Leibniz brought these techniques together through the derivative (the curve of mathematical function) and integral (the area under the curve). Though their methods were not always logically sound, mathematicians in the 18th century took on the rigorization stage and were able to justify their methods and create the final stage of calculus. Today, we define the derivative and integral in terms of limits.

In contrast to calculus, which is a type of continuous mathematics (dealing with real numbers), other mathematicians have taken a more theoretical approach. Discrete mathematics is the branch of math that deals with objects that can assume only distinct, separated value, as mathematician and computer scientist Richard Johnsonbaugh explained in " Discrete Mathematics " (Pearson, 2017). Discrete objects can be characterized by integers, rather than real numbers. Discrete mathematics is the mathematical language of computer science, as it includes the study of algorithms. Fields of discrete mathematics include combinatorics, graph theory and the theory of computation.

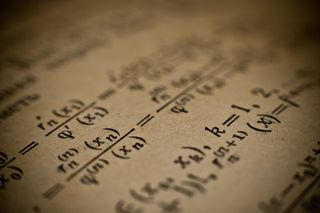
Why mathematics is important

It's not uncommon for people to wonder what relevance mathematics serves in their daily lives. In the modern world, math such as applied mathematics is not only relevant, it's crucial. Applied mathematics covers the branches that study the physical, biological or sociological world. 

"The goal of applied mathematics is to establish the connections between separate academic fields," wrote Alain Goriely in " Applied Mathematics: A Very Short Introduction " (Oxford University Press, 2018). Modern areas of applied math include mathematical physics, mathematical biology, control theory, aerospace engineering and math finance. Not only does applied math solve problems, but it also discovers new problems or develops new engineering disciplines, Goriely added. The common approach in applied math is to build a mathematical model of a phenomenon, solve the model and develop recommendations for performance improvement.

While not necessarily an opposite to applied mathematics, pure mathematics is driven by abstract problems, rather than real-world problems. Much of the subjects that are pursued by pure mathematicians have their roots in concrete physical problems, but a deeper understanding of these phenomena brings about problems and technicalities. 

These abstract problems and technicalities are what pure mathematics attempts to solve, and these attempts have led to major discoveries for humankind, including the universal Turing machine, theorized by Alan Turing in 1937. This machine, which began as an abstract idea, later laid the groundwork for the development of modern computers. Pure mathematics is abstract and based in theory, and is thus not constrained by the limitations of the physical world.

According to Goriely, "Applied mathematics is to pure mathematics, what pop music is to classical music." Pure and applied are not mutually exclusive, but they are rooted in different areas of math and problem solving. Though the complex math involved in pure and applied mathematics is beyond the understanding of most people, the solutions developed from the processes have affected and improved the lives of many.

Originally published on Live Science .

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

A Prime Day telescope deal so good we bought one for ourselves

Samsung Galaxy Watch now at lowest-ever price in this Prime Day deal

How old is planet Earth?

Most Popular

• 2 Euclid telescope reveals 1st section of largest-ever 3D map of the universe — and there's still 99% to go
• 3 1st wheel was invented 6,000 years ago in the Carpathian Mountains, modeling study suggests
• 4 Doctors no longer recommend 'self-checks' for breast cancer — here's what to know
• 5 Key Atlantic current could collapse soon, 'impacting the entire world for centuries to come,' leading climate scientists warn

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Mathematics

The science of quantitative relations and spatial forms in the real world. Being inseparably connected with the needs of technology and natural science, the accumulation of quantitative relations and spatial forms studied in mathematics is continuously expanding; so this general definition of mathematics becomes ever richer in content.

The clear recognition of the independent position of mathematics as a separate science became possible only after the collection of a fairly large store of factual material, and arose first in Ancient Greece in the 6th–5th centuries B.C.. The development of mathematics up to that time is naturally referred to as the period of the origin of mathematics, and the 6th–5th centuries B.C. as the beginning of the period of elementary mathematics. During these first two periods mathematical investigation dealt almost exclusively with very restricted questions concerning fundamental ideas, already there in the very early stages of historical development in relation with very simple aspects of economic life. The first problems of mechanics and physics were already in this collection of fundamental mathematical ideas.

In the 17th century new questions in natural science and technology compelled mathematicians to concentrate their attention on the creation of methods to allow the mathematical study of motion, the processes of variation of quantities and the transformation of geometrical figures. With the use of variable quantities in analytic geometry and the creation of differential and integral calculus, the period of the mathematics of variable quantities began.

Further expansion of the circle of quantitative relations and spatial forms studied in mathematics led, at the beginning of the 19th century, to the need to consciously regard the very process of expansion as a topic of mathematical research by setting the problem of systematically studying, from a fairly general point of view, the possible types of quantitative relations and spatial forms. The creation of the "imaginary" geometry of Lobachevskii was the first significant step in this direction. The development of this type of research introduced such an important new feature into mathematics that mathematics in the 19th century and 20th century is naturally referred to as the special period of modern mathematics.

• 1 1. The origin of mathematics.
• 2 2. The period of elementary mathematics.
• 3 3. The period of creation of the mathematics of variable quantities.
• 4.1 References
• 4.2 Comments
• 4.3 References

1. The origin of mathematics.

Consideration of the objects in the very early stages in the development of cultures leads to the creation of the simplest ideas of the arithmetic of natural numbers. Based on an elaborate system of verbal calculation, written systems of calculation arose and slowly the methods of doing the four arithmetic operations over the natural numbers were perfected. The demands of measurement (quantity of grain, length of a road, etc.) led to the emergence of names and notation for the simplest fractions and to the elaboration of methods for performing arithmetic operations on fractions. In this way material was accumulated which gradually added up to that most ancient mathematical science: arithmetic . The measurement of area and volume, the needs of building technology and, somewhat later, astronomy motivated the development of the rudiments of geometry . These processes occurred in many nations, largely independently and in parallel. Of special significance for the later development of science was the accumulation of arithmetic and geometric knowledge in Egypt and Babylon. In Babylon, on the basis of the techniques which were developed for arithmetic calculation, algebra appeared also in connection with the needs of astronomy, and the rudiments of trigonometry appeared.

2. The period of elementary mathematics.

Only after the accumulation of a larger amount of concrete material in the form of un-coordinated methods of arithmetic calculation and methods for determining area and volume, did mathematics arise as an independent science with a clear understanding of the originality of its method and the necessity for a systematic development of its basic concepts and assumptions in a fairly general form. In the application to arithmetic and algebra this process had already begun in Babylon. However, this new trend, comprising the systematic and logical succession of the construction of the foundations of mathematics, was fully defined in Ancient Greece. The system of exposition of elementary geometry created by the Ancient Greeks remained for more than two thousand years the standard for the deductive construction of a mathematical theory. From arithmetic gradually grew number theory . The systematic study of magnitudes and measurements was created. The process of forming (in connection with the problems of measurement of magnitude) the notion of a real number (see Number ) turned out to be very protracted. The problem was that the idea of an irrational or a negative number was related to more complicated mathematical abstractions which, in contrast to the concepts of a natural number, a fraction or a geometric figure, have no fairly sound support in prescientific ordinary human experience. The creation of algebra as a literal calculus was completed only at the end of this period. The period of elementary mathematics ended (in Western Europe at the beginning of the 17th century), when the emphasis of mathematical interests shifted to the domain of mathematics of variable quantities.

3. The period of creation of the mathematics of variable quantities.

With the 17th century an essentially new period in the development of mathematics began. The circle of quantitative relations and spatial forms of mathematics studied now was no longer exhausted by numbers, quantities and geometric figures. On this basis there resulted the explicit introduction into mathematics of the ideas of motions and change. Already algebra contained the idea of dependence between variables in a latent form (the value of a sum depends on the values of the terms, etc.). However, in order to include quantitative relations in the process of variation it was necessary that the very dependence between the variables be made an independent object of study. Therefore, in the first scheme the notion of a function was put forward, which later played the same role of fundamental and independent object of study as the notion of quantity or number had played earlier. The study of variable quantities and functional dependence leads to the fundamental ideas of mathematical analysis, introducing explicitly into mathematics the idea of the infinite, the notions of a limit, a derivative, a differential, and an integral. Infinitesimal analysis was born; in the first place in the form of the differential calculus and integral calculus , allowing one to relate finite variations of variable quantities to their behaviour in an immediate vicinity of their individual values. The basic laws of mechanics and physics were described by differential equations, and the problem of investigating these equations comes to the foreground as one of the major problems of mathematics. The search for unknown functions defined by conditions of another kind (conditions of maxima or minima of certain related quantities) forms the topic of the calculus of variations (cf. Variational calculus ). In this way, side-by-side with equations in which the unknowns are numbers, equations emerge in which functions are the unknowns and have to be determined.

The subject of geometry is also significantly expanded with the penetration into geometry of the ideas of motions and transformations of figures. Geometry begins to study motions and transformations for their own sake. For example, in projective geometry one of the basic objects of study is the set of projective transformations of the plane or space. However, the conscious development of these ideas dates only from the end of the 18th century and the beginning of the 19th century. Much earlier, with the advent of analytic geometry in the 17th century, the relation of geometry to the remainder of mathematics was essentially changed; a universal method was found for transferring questions of geometry into the language of algebra and analysis and for solving them neatly by algebraic and analytic methods. On the other hand, the broad possibility of sketching (illustrating) algebraic and analytic facts by geometric means was discovered, for example, in the graphical illustration of functional dependence.

4. Modern mathematics.

All the divisions of mathematical analysis created in the 17th century and 18th century continued to develop with great intensity in the 19th century and 20th century. The circle of applications to problems of science and technology was greatly expanded at this time. However, in addition to this quantitative growth, at the end of the 18th century and the beginning of the 19th century a number of essentially new features were observed in the development of mathematics.

The enormous amount of factual material which had been accumulated in the 17th century and 18th century led to the demand for a deep logical analysis and unification of it from a new point of view. In essence, the relationship between mathematics and natural science was no less close but was now increased in complexity. The majority of new theories arose not just as a result of the immediate needs of natural science and technology, but also from internal requirements of mathematics itself. Such, in essence, was the development of the theory of functions of a complex variable (cf. Functions of a complex variable, theory of ), which occupied a central position in mathematical analysis at the beginning and middle of the 19th century. Another remarkable example of a theory arising as a result of the internal development of mathematics was Lobachevskii geometry .

In more immediate and continuous relation to the needs of mechanics and physics the formation of vector and tensor calculus arose. The translation of vector and tensor notions into infinite-dimensional quantities resulted in the framework of functional analysis and is closely connected with the requirements of modern physics.

In this way, as a result of both the internal requirements of mathematics and the new needs of natural science, the circle of quantitative relations and spatial forms studied in mathematics was greatly expanded: relations between elements of arbitrary groups, operations in function spaces, the whole diversity of forms of spaces of any number of dimensions, etc. are now parts of mathematics.

The essential novelty of this stage in the development of mathematics, beginning in the 19th century, is that questions concerning the necessary expansion of the circle of ideas in the study of quantitative relations and spatial forms themselves became the subject of conscious and active interest for mathematicians. If before, for example, the introduction of negative and complex numbers and the exact formulation of their rules of operation required protracted effort, now the development of mathematics required elaboration of methods for the deliberate and planned creation of new geometric and algebraic systems.

The extraordinary expansion of the subject of mathematics in the 19th century attracted vigorous attention to the question of its "foundations" , that is, a critical review of its initial conditions (axioms), the construction of rigorous systems of definitions and proofs and also a critical consideration of the logical methods used in these proofs. The standard requirement of logical rigour imposed on the practical work of mathematicians in the development of individual mathematical theories was added only at the end of the 19th century. A deep and careful analysis of the requirement of logical rigour in proofs, the construction of mathematical theories, questions of algorithmic solvability and unsolvability of mathematical problems, comprise the subject of mathematical logic .

At the beginning of the 19th century a new significant expansion of the domain of application of mathematical analysis was initiated. Up to this time the fundamental divisions of physics demanding the greatest mathematical apparatus were mechanics and optics. Now were added electrodynamics and the theories of magnetism and thermodynamics. The important division of the mechanics of continuous media underwent broad development. The mathematical needs of technology also grew rapidly. As the fundamental apparatus of the new areas of mechanics and mathematical physics, the theories of ordinary and partial differential equations and of the equations of mathematical physics were strongly developed (cf. Differential equation, ordinary ; Differential equation, partial ; Mathematical physics, equations of ).

The theory of differential equations served as the starting point for the investigation of the topology of manifolds. Here were obtained the first "combinatorial" , "homological" and "homotopical" methods of algebraic topology . Another direction in topology arose, based on set theory and functional analysis , and has led to the systematic construction of the theory of general topological spaces (cf. Topological space ).

An essential completion to the methods of differential equations in the study of the character and solution of technical problems are the methods of probability theory . If at the beginning of the 19th century the principal use of probabilistic methods was in ballistics and the theory of errors, then at the end of the 19th century and the beginning of the 20th century probability theory had many applications, due to the creation of the theory of random processes and the development of the apparatus of mathematical statistics .

The theory of numbers, a collection of diverse results and ideas, was developed in various directions in the 19th century as a structured theory (see Algebraic number theory ; Analytic number theory ; Diophantine approximations ).

The emphasis of algebraic research shifted to new areas of algebra: the theory of groups, rings, fields, and general algebraic structures. On the interface between algebra and geometry grew the theory of continuous groups, the methods of which later permeated into all new areas of mathematics and natural science.

Elementary and projective geometry attracted the attention of mathematicians mainly from the point of the study of logical and axiomatic foundations. But the fundamental areas of geometry on which most of the significant scientific force was concentrated became differential geometry ; algebraic geometry and Riemannian geometry .

As a result of the systematic construction of mathematical analysis based on the strictly arithmetic theory of irrational numbers and on set theory, the theory of functions of a real variable arose (cf. Functions of a real variable, theory of ).

The practical application of the results of pure mathematical research required obtaining an answer to a given problem in numerical form. However, even after exhaustive theoretical analysis of a problem this often turns out to be a very difficult matter. The numerical methods of analysis and algebra that arose at the end of the 19th century and the beginning of the 20th century have grown with the manufacture and use of computers into an independent branch of mathematics: computational mathematics .

These fundamental distinctive features of modern mathematics and the basic directions of research within the divisions of mathematics are listed as at the beginning of the 20th century. To a large extent this division into branches has been preserved in spite of the tremendous growth of mathematics in the 20th century. However, the demand for the development of mathematics itself, the "mathematization" of various domains of science, the penetration of mathematical methods into many spheres of practical activity, and the rapid progress in computational techniques has led to a mixing of the basic efforts of mathematicians over the branches of mathematics and to the appearance of a whole series of new mathematical disciplines (see, for example, Automata, theory of ; Information theory ; Games, theory of ; Operations research , and also Cybernetics ; Mathematical economics ). On the basis of problems in the theory of control systems (cf. Control system ), combinatorial analysis, graph theory, coding theory, and discrete analysis arose. Questions on optimal (in some sense) control of physical or mechanical systems described by differential equations has led to the creation of the mathematical theory of optimal control (cf. Optimal control, mathematical theory of ).

Studies in the domain of general control problems and related areas of mathematics, in conjunction with the progress in computational techniques, provided a basis for the automatization of new spheres of human activity.

• This page was last edited on 30 March 2012, at 21:54.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

How to Write a Math Essay

Students often wonder why they have to write in math class. In fact, the purpose of a math essay is for students to demonstrate their understanding of mathematical ideas and concepts. Both high school and college students have to write math essays. Though it is a specific type of writing, you can follow many of the same guidelines for writing used in other subjects.

The first step to writing a math essay is choosing a topic. One option is to choose a mathematical concept you find interesting, such as one which you discussed in class but want to explore further. Alternatively, choose a problem that you've solved. For this type of essay, you state the problem and solution and explain how you arrived at the answer. For either type of essay, brainstorm what about the topic or problem intrigues you. For example, consider why you chose to delve deeper into that particular concept or explain the math for that specific equation.

Advertisement

Article continues below this ad

Just like essays in other subjects, math essays require you to consider your audience. Mathematician P.R. Halmos suggests in his article, "How to Write Mathematics," thinking of a particular person when writing, especially one whose math ways "can stand mending." Therefore, unless directed otherwise, write as if your audience has the same basic level of math skills as you. Though you are writing a math essay to explain an idea or solution, you also want to persuade your reader that your methodology is the best one. Keep in mind your professor or teacher is not the main audience member as he already understands the concept.

More For You

How to write a shrinklet poem, how to develop and write a paragraph, describe the elements of a good & bad thesis statement, how to write a pros & cons essay, how to write an essay for the ged test, concept essay organization.

A math essay about a concept looks similar to essays in other classes; it is, in fact, an expository essay. For this, you investigate a mathematical concept, develop further ideas about the theory based on research and make a claim in the form of a thesis statement. To write the essay, start with an introduction by stating the topic and its import. The introduction includes your claim about the theory. Develop the claim in subsequent paragraphs using evidence from your research as support. Conclude by tying up any loose ends and readdressing the theory in light of the information you provided.

Equation Essay Organization

For an equation essay, state the problem and solution directly in the introduction; explain the significance of the problem and your rationale for solving it as you did. The significance and rationale are similar to a thesis statement, providing the basis for your argument. Write a paragraph clearly explaining how you approach the problem, thus giving the reader a guide to follow. For a complex problem, include a graph that helps demonstrate the result of your equation, explaining explicitly what the graph shows. Similarly, define variables precisely with phrases such as "Let n be any real number." Describe your method for solving the problem, guiding your reader through the formulas you used and your reasons for using them.

• University of California, Davis: A Guide to Writing Mathematics
• Oregon State University: How to Write a Math Essay
• Purdue Online Writing Lab: Expository Essays

Nadia Archuleta has a B.A. in English writing. She spent five years working abroad and has traveled extensively. She has worked as an English as a Foreign/Second Language teacher for 12 years.