

Defining and measuring oligopoly
Concentration ratios
Example of a hypothetical concentration ratio, fixed broadband services, fuel retailing, further examples, the herfindahl – hirschman index (h-h index), key characteristics, interdependence.
- Whether to compete with rivals, or collude with them.
- Whether to raise or lower price, or keep price constant.
- Whether to be the first firm to implement a new strategy, or whether to wait and see what rivals do. The advantages of ‘going first’ or ‘going second’ are respectively called 1st and 2nd-mover advantage. Sometimes it pays to go first because a firm can generate head-start profits. 2nd mover advantage occurs when it pays to wait and see what new strategies are launched by rivals, and then try to improve on them or find ways to undermine them.
Barriers to entry
Natural entry barriers include:, economies of large scale production., ownership or control of a key scarce resource, high set-up costs, high r&d costs, artificial barriers include:, predatory pricing, limit pricing, superior knowledge, predatory acquisition, advertising, a strong brand, loyalty schemes, exclusive contracts, patents and licences, vertical integration, collusive oligopolies, types of collusion, competitive oligopolies, pricing strategies of oligopolies.
- Oligopolists may use predatory pricing to force rivals out of the market. This means keeping price artificially low, and often below the full cost of production.
- They may also operate a limit-pricing strategy to deter entrants, which is also called entry forestalling price .
- Oligopolists may collude with rivals and raise price together, but this may attract new entrants.
- Cost-plus pricing is a straightforward pricing method, where a firm sets a price by calculating average production costs and then adding a fixed mark-up to achieve a desired profit level. Cost-plus pricing is also called rule of thumb pricing.There are different versions of cost-pus pricing, including full cost pricing , where all costs - that is, fixed and variable costs - are calculated, plus a mark up for profits, and contribution pricing , where only variable costs are calculated with precision and the mark-up is a contribution to both fixed costs and profits.

Non-price strategies
- Trying to improve quality and after sales servicing, such as offering extended guarantees.
- Spending on advertising, sponsorship and product placement - also called hidden advertising – is very significant to many oligopolists. The UK's football Premiership has long been sponsored by firms in oligopolies, including Barclays Bank and Carling.
- Sales promotion, such as buy-one-get-one-free (BOGOF), is associated with the large supermarkets, which is a highly oligopolistic market, dominated by three or four large chains.
- Loyalty schemes, which are common in the supermarket sector, such as Sainsbury’s Nectar Card and Tesco’s Club Card .
- How successful is it likely to be?
- Will rivals be able to copy the strategy?
- Will the firms get a 1st - mover advantage?
- How expensive is it to introduce the strategy? If the cost of implementation is greater than the pay-off, clearly it will be rejected.
- How long will it take to work? A strategy that takes five years to generate a pay-off may be rejected in favour of a strategy with a quicker pay-off.
Price stickiness
Kinked demand curve.

Maximising profits
A game theory approach to price stickiness.
- Raise price
- Lower price
- Keep price constant
The Prisoner’s Dilemma
- Higher prices or hidden prices, such as the hidden charges in credit card transactions
- Lower output
- Restricted choice or other limiting conditions associated with the transaction
Examples of Oligopoly
Evaluation of oligopolies, the disadvantages of oligopolies.
- High concentration reduces consumer choice.
- Cartel-like behaviour reduces competition and can lead to higher prices and reduced output.
- Given the lack of competition, oligopolists may be free to engage in the manipulation of consumer decision making. By making decisions more complex - such as financial decisions about mortgages - individual consumers fall back on heuristics and rule of thumb processes, which can lead to decision making bias and irrational behaviour, including making purchases which add no utility or even harm the individual consumer.
- Firms can be prevented from entering a market because of deliberate barriers to entry .
- There is a potential loss of economic welfare.
- Oligopolists may be allocatively and productively inefficient .

The advantages of oligopolies
- Oligopolies may adopt a highly competitive strategy, in which case they can generate similar benefits to more competitive market structures , such as lower prices. Even though there are a few firms, making the market uncompetitive, their behaviour may be highly competitive.
- Oligopolists may be dynamically efficient in terms of innovation and new product and process development. The super-normal profits they generate may be used to innovate, in which case the consumer may gain.
- Price stability may bring advantages to consumers and the macro-economy because it helps consumers plan ahead and stabilises their expenditure, which may help stabilise the trade cycle.
Test your knowledge with a quiz
Press next to launch the quiz, you are allowed two attempts - feedback is provided after each question is attempted..

Game Theory

Monopolistic competition

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
11.2 Oligopoly: Competition Among the Few
Learning objectives.
- Explain the main characteristics of an oligopoly, differentiating it from other types of market structures.
- Explain the measures that are used to determine the degree of concentration in an industry.
- Explain and illustrate the collusion model of oligopoly.
- Discuss how game theory can be used to understand the behavior of firms in an oligopoly.
In July, 2005, General Motors Corporation (GMC) offered “employee discount pricing” to virtually all GMC customers, not just employees and their relatives. This new marketing strategy introduced by GMC obviously affected Ford, Chrysler, Toyota and other automobile and truck manufacturers; Ford matched GMC’s employee-discount plan by offering up to $1,000 to its own employees who convinced friends to purchase its cars and trucks. Ford also offered its customers the same prices paid by its employees. By mid-July, Chrysler indicated that it was looking at many alternatives, but was waiting for GMC to make its next move. Ultimately, Chrysler also offered employee discount pricing.
Toyota had to respond. It quickly developed a new marketing strategy of its own, which included lowering the prices of its cars and offering new financing terms. The responses of Ford, Chrysler, and Toyota to GMC’s pricing strategy obviously affected the outcome of that strategy. Similarly, a decision by Procter & Gamble to lower the price of Crest toothpaste may elicit a response from Colgate-Palmolive, and that response will affect the sales of Crest. In an oligopoly , the fourth and final market structure that we will study, the market is dominated by a few firms, each of which recognizes that its own actions will produce a response from its rivals and that those responses will affect it.
The firms that dominate an oligopoly recognize that they are interdependent: What one firm does affects each of the others. This interdependence stands in sharp contrast to the models of perfect competition and monopolistic competition, where we assume that each firm is so small that it assumes the rest of the market will, in effect, ignore what it does. A perfectly competitive firm responds to the market, not to the actions of any other firm. A monopolistically competitive firm responds to its own demand, not to the actions of specific rivals. These presumptions greatly simplify the analysis of perfect competition and monopolistic competition. We do not have that luxury in oligopoly, where the interdependence of firms is the defining characteristic of the market.
Some oligopoly industries make standardized products: steel, aluminum, wire, and industrial tools. Others make differentiated products: cigarettes, automobiles, computers, ready-to-eat breakfast cereal, and soft drinks.
Measuring Concentration in Oligopoly
Oligopoly means that a few firms dominate an industry. But how many is “a few,” and how large a share of industry output does it take to “dominate” the industry?
Compare, for example, the ready-to-eat breakfast cereal industry and the ice cream industry. The cereal market is dominated by two firms, Kellogg’s and General Mills, which together hold more than half the cereal market. This oligopoly operates in a highly concentrated market. The market for ice cream, where the four largest firms account for just less than a third of output, is much less concentrated.
One way to measure the degree to which output in an industry is concentrated among a few firms is to use a concentration ratio , which reports the percentage of output accounted for by the largest firms in an industry. The higher the concentration ratio, the more the firms in the industry take account of their rivals’ behavior. The lower the concentration ratio, the more the industry reflects the characteristics of monopolistic competition or perfect competition.
The U.S. Census Bureau, based on surveys it conducts of manufacturing firms every five years, reports concentration ratios. These surveys show concentration ratios for the largest 4, 8, 20, and 50 firms in each industry category. Some concentration ratios from the 2002 survey, the latest available, are reported in Table 11.1 “Concentration Ratios and Herfindahl–Hirschman Indexes” . Notice that the four-firm concentration ratio for breakfast cereals is 78%; for ice cream it is 48%.
Table 11.1 Concentration Ratios and Herfindahl–Hirschman Indexes
| Industry | Largest 4 firms | Largest 8 firms | Largest 20 firms | Largest 50 firms | HHI |
|---|---|---|---|---|---|
| Ice cream | 48 | 64 | 82 | 93 | 736 |
| Breakfast cereals | 78 | 91 | 99 | 100 | 2521 |
| Cigarettes | 95 | 99 | 100 | *D | |
| Men’s and boys’ shirts | 38 | 53 | 73 | 89 | 481 |
| Women’s and girls’ blouses and shirts | 21 | 32 | 49 | 70 | 186 |
| Automobiles | 76 | 94 | 99 | 100 | 1911 |
| Sporting and athletic goods | 23 | 32 | 46 | 62 | 182 |
| Dental laboratories | 13 | 18 | 23 | 30 | 54 |
| *D, data withheld by the government to avoid revealing information about specific firms. | |||||
Two measures of industry concentration are reported by the Census Bureau: concentration ratios and the Herfindahl–Hirschman Index (HHI).
Source: Selected statistics from Sector 31: Manufacturing: Subject Series—Concentration Ratios: Share of Value of Shipments Accounted for by the 4, 8, 20, and 50 Largest Companies for Industries: 2002 at http://www.census.gov/epcd/www/concentration.html .
An alternative measure of concentration is found by squaring the percentage share (stated as a whole number) of each firm in an industry, then summing these squared market shares to derive a Herfindahl–Hirschman Index (HHI) . The largest HHI possible is the case of monopoly, where one firm has 100% of the market; the index is 100 2 , or 10,000. An industry with two firms, each with 50% of total output, has an HHI of 5,000 (50 2 + 50 2 ). In an industry with 10,000 firms that have 0.01% of the market each, the HHI is 1. Herfindahl–Hirschman Indexes reported by the Census Bureau are also given in Table 11.1 “Concentration Ratios and Herfindahl–Hirschman Indexes” . Notice that the HHI is 2,521 for breakfast cereals and only 736 for ice cream, suggesting that the ice cream industry is more competitive than the breakfast cereal industry.
In some cases, the census data understate the degree to which a few firms dominate the market. One problem is that industry categories may be too broad to capture significant cases of industry dominance. The sporting goods industry, for example, appears to be highly competitive if we look just at measures of concentration, but markets for individual goods, such as golf clubs, running shoes, and tennis rackets, tend to be dominated by a few firms. Further, the data reflect shares of the national market. A tendency for regional domination does not show up. For example, the concrete industry appears to be highly competitive. But concrete is produced in local markets—it is too expensive to ship it very far—and many of these local markets are dominated by a handful of firms.
The census data can also overstate the degree of actual concentration. The “automobiles” category, for example, has a four-firm concentration ratio that suggests the industry is strongly dominated by four large firms (in fact, U.S. production is dominated by three: General Motors, Ford, and Chrysler). Those firms hardly account for all car sales in the United States, however, as other foreign producers have captured a large portion of the domestic market. Including those foreign competitors suggests a far less concentrated industry than the census data imply.
The Collusion Model
There is no single model of profit-maximizing oligopoly behavior that corresponds to economists’ models of perfect competition, monopoly, and monopolistic competition. Uncertainty about the interaction of rival firms makes specification of a single model of oligopoly impossible. Instead, economists have devised a variety of models that deal with the uncertain nature of rivals’ responses in different ways. In this section we review one type of oligopoly model, the collusion model. After examining this traditional approach to the analysis of oligopoly behavior, we shall turn to another method of examining oligopolistic interaction: game theory.
Firms in any industry could achieve the maximum profit attainable if they all agreed to select the monopoly price and output and to share the profits. One approach to the analysis of oligopoly is to assume that firms in the industry collude, selecting the monopoly solution.
Suppose an industry is a duopoly , an industry with two firms. Figure 11.5 “Monopoly Through Collusion” shows a case in which the two firms are identical. They sell identical products and face identical demand and cost conditions. To simplify the analysis, we will assume that each has a horizontal marginal cost curve, MC. The demand and marginal revenue curves are the same for both firms. We find the combined demand curve for the two firms, D combined , by adding the individual demand curves together. Because one firm’s demand curve, D firm , represents one-half of market demand, it is the same as the combined marginal revenue curve for the two firms. If these two firms act as a monopoly, together they produce Q m and charge a price P m . This result is achieved if each firm selects its profit-maximizing output, which equals 1/2 Q m . This solution is inefficient; the efficient solution is price P c and output Q c , found where the combined market demand curve D combined and the marginal cost curve MC intersect.
Figure 11.5 Monopoly Through Collusion
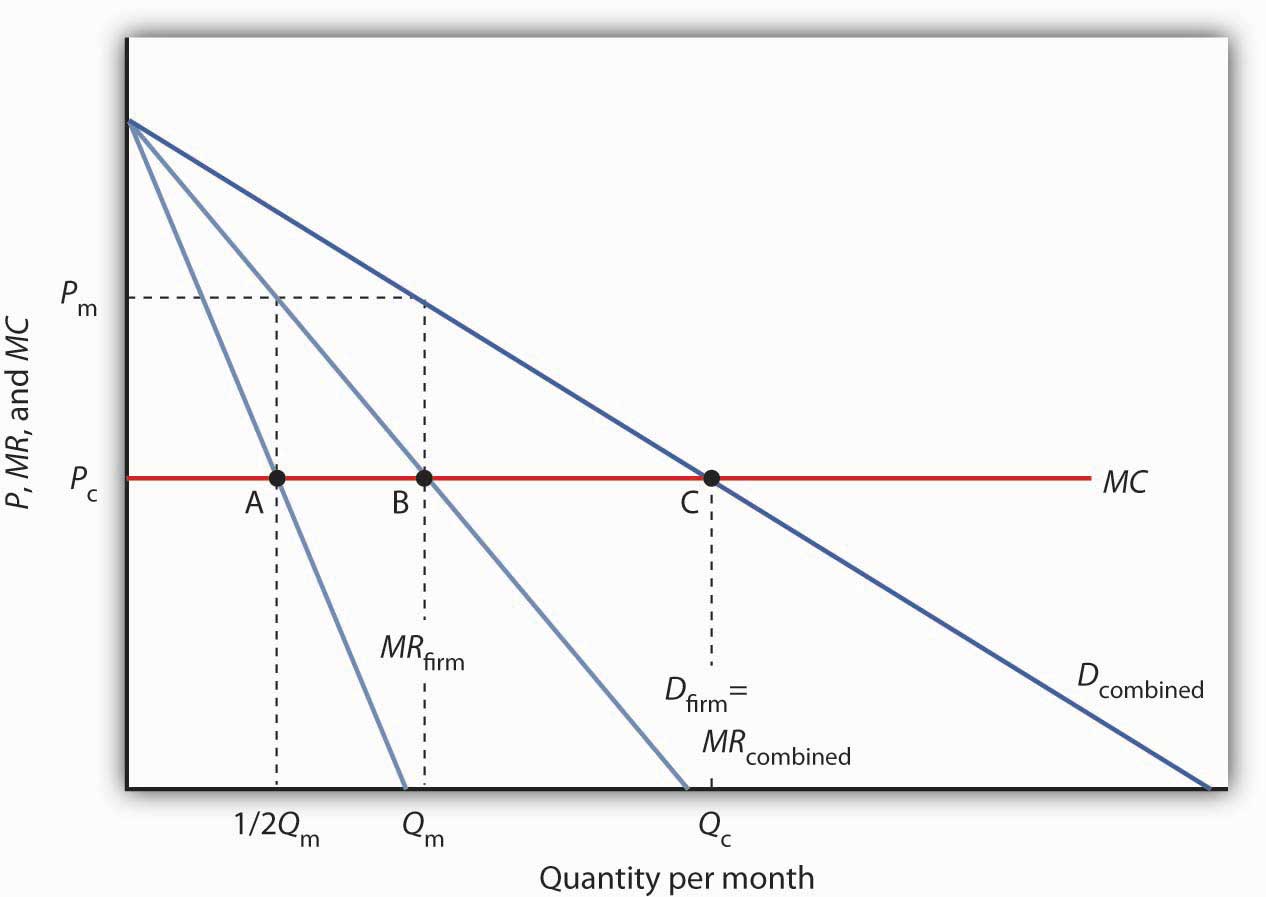
Two identical firms have the same horizontal marginal cost curve MC. Their demand curves D firm and marginal revenue curves MR firm are also identical. The combined demand curve is D combined ; the combined marginal revenue curve is MR combined . The profits of the two firms are maximized if each produces 1/2 Q m at point A. Industry output at point B is thus Q m and the price is P m . At point C, the efficient solution output would be Q c , and the price would equal MC .
In the simplest form of collusion, overt collusion , firms openly agree on price, output, and other decisions aimed at achieving monopoly profits. Firms that coordinate their activities through overt collusion and by forming collusive coordinating mechanisms make up a cartel .
Firms form a cartel to gain monopoly power. A successful cartel can earn large profits, but there are several problems with forming and maintaining one. First, in many countries, including the United States, cartels are generally illegal 1 . They are banned, because their purpose is to raise prices and restrict output. Second, the cartel may not succeed in inducing all firms in the industry to join. Firms that remain outside the cartel can compete by lowering price, and thus they prevent the cartel from achieving the monopoly solution. Third, there is always an incentive for individual members to cheat on cartel agreements. Suppose the members of a cartel have agreed to impose the monopoly price in their market and to limit their output accordingly. Any one firm might calculate that it could charge slightly less than the cartel price and thus capture a larger share of the market for itself. Cheating firms expand output and drive prices down below the level originally chosen.
The Organization of Petroleum Exporting Countries (OPEC), perhaps the best-known cartel, is made up of 13 oil-producing countries. In the 1970s, OPEC successfully acted like a monopoly by restricting output and raising prices. By the mid-1980s, however, the monopoly power of the cartel had been weakened by expansion of output by nonmember producers such as Mexico and Norway and by cheating among the cartel members.
An alternative to overt collusion is tacit collusion , an unwritten, unspoken understanding through which firms agree to limit their competition. Firms may, for example, begin following the price leadership of a particular firm, raising or lowering their prices when the leader makes such a change. The price leader may be the largest firm in the industry, or it may be a firm that has been particularly good at assessing changes in demand or cost. At various times, tacit collusion has been alleged to occur in a wide range of industries, including steel, cars, and breakfast cereals.
It is difficult to know how common tacit collusion is. The fact that one firm changes its price shortly after another one does cannot prove that a tacit conspiracy exists. After all, we expect to see the prices of all firms in a perfectly competitive industry moving together in response to changes in demand or production costs.
Game Theory and Oligopoly Behavior
Oligopoly presents a problem in which decision makers must select strategies by taking into account the responses of their rivals, which they cannot know for sure in advance. The Start Up feature at the beginning of this chapter suggested the uncertainty eBay faces as it considers the possibility of competition from Google. A choice based on the recognition that the actions of others will affect the outcome of the choice and that takes these possible actions into account is called a strategic choice . Game theory is an analytical approach through which strategic choices can be assessed.
Among the strategic choices available to an oligopoly firm are pricing choices, marketing strategies, and product-development efforts. An airline’s decision to raise or lower its fares—or to leave them unchanged—is a strategic choice. The other airlines’ decision to match or ignore their rival’s price decision is also a strategic choice. IBM boosted its share in the highly competitive personal computer market in large part because a strategic product-development strategy accelerated the firm’s introduction of new products.
Once a firm implements a strategic decision, there will be an outcome. The outcome of a strategic decision is called a payoff . In general, the payoff in an oligopoly game is the change in economic profit to each firm. The firm’s payoff depends partly on the strategic choice it makes and partly on the strategic choices of its rivals. Some firms in the airline industry, for example, raised their fares in 2005, expecting to enjoy increased profits as a result. They changed their strategic choices when other airlines chose to slash their fares, and all firms ended up with a payoff of lower profits—many went into bankruptcy.
We shall use two applications to examine the basic concepts of game theory. The first examines a classic game theory problem called the prisoners’ dilemma. The second deals with strategic choices by two firms in a duopoly.
The Prisoners’ Dilemma
Suppose a local district attorney (DA) is certain that two individuals, Frankie and Johnny, have committed a burglary, but she has no evidence that would be admissible in court.
The DA arrests the two. On being searched, each is discovered to have a small amount of cocaine. The DA now has a sure conviction on a possession of cocaine charge, but she will get a conviction on the burglary charge only if at least one of the prisoners confesses and implicates the other.
The DA decides on a strategy designed to elicit confessions. She separates the two prisoners and then offers each the following deal: “If you confess and your partner doesn’t, you will get the minimum sentence of one year in jail on the possession and burglary charges. If you both confess, your sentence will be three years in jail. If your partner confesses and you do not, the plea bargain is off and you will get six years in prison. If neither of you confesses, you will each get two years in prison on the drug charge.”
The two prisoners each face a dilemma; they can choose to confess or not confess. Because the prisoners are separated, they cannot plot a joint strategy. Each must make a strategic choice in isolation.
The outcomes of these strategic choices, as outlined by the DA, depend on the strategic choice made by the other prisoner. The payoff matrix for this game is given in Figure 11.6 “Payoff Matrix for the Prisoners’ Dilemma” . The two rows represent Frankie’s strategic choices; she may confess or not confess. The two columns represent Johnny’s strategic choices; he may confess or not confess. There are four possible outcomes: Frankie and Johnny both confess (cell A), Frankie confesses but Johnny does not (cell B), Frankie does not confess but Johnny does (cell C), and neither Frankie nor Johnny confesses (cell D). The portion at the lower left in each cell shows Frankie’s payoff; the shaded portion at the upper right shows Johnny’s payoff.
Figure 11.6 Payoff Matrix for the Prisoners’ Dilemma
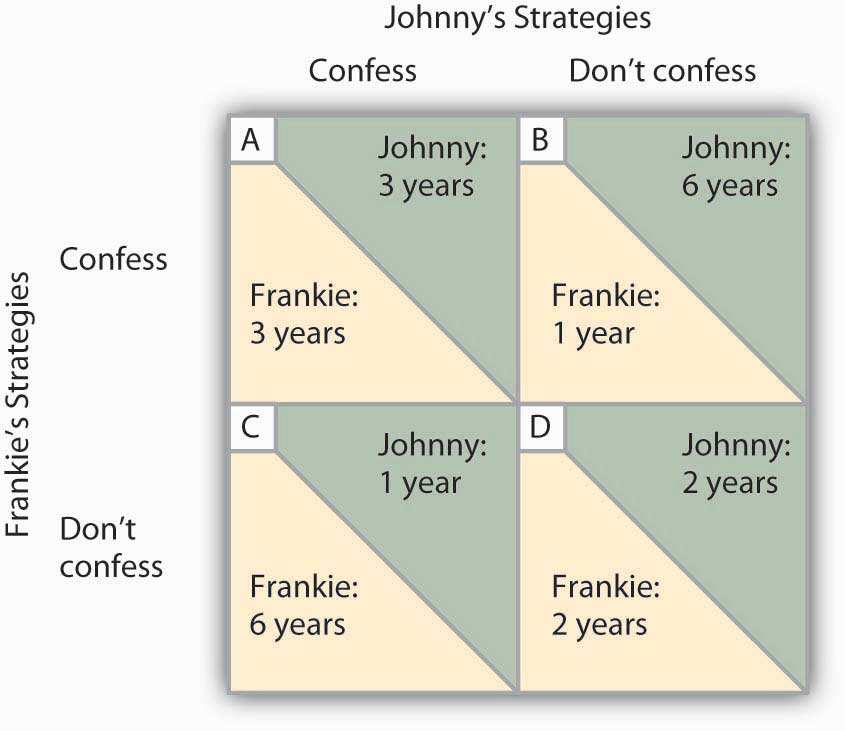
The four cells represent each of the possible outcomes of the prisoners’ game.
If Johnny confesses, Frankie’s best choice is to confess—she will get a three-year sentence rather than the six-year sentence she would get if she did not confess. If Johnny does not confess, Frankie’s best strategy is still to confess—she will get a one-year rather than a two-year sentence. In this game, Frankie’s best strategy is to confess, regardless of what Johnny does. When a player’s best strategy is the same regardless of the action of the other player, that strategy is said to be a dominant strategy . Frankie’s dominant strategy is to confess to the burglary.
For Johnny, the best strategy to follow, if Frankie confesses, is to confess. The best strategy to follow if Frankie does not confess is also to confess. Confessing is a dominant strategy for Johnny as well. A game in which there is a dominant strategy for each player is called a dominant strategy equilibrium . Here, the dominant strategy equilibrium is for both prisoners to confess; the payoff will be given by cell A in the payoff matrix.
From the point of view of the two prisoners together, a payoff in cell D would have been preferable. Had they both denied participation in the robbery, their combined sentence would have been four years in prison—two years each. Indeed, cell D offers the lowest combined prison time of any of the outcomes in the payoff matrix. But because the prisoners cannot communicate, each is likely to make a strategic choice that results in a more costly outcome. Of course, the outcome of the game depends on the way the payoff matrix is structured.
Repeated Oligopoly Games
The prisoners’ dilemma was played once, by two players. The players were given a payoff matrix; each could make one choice, and the game ended after the first round of choices.
The real world of oligopoly has as many players as there are firms in the industry. They play round after round: a firm raises its price, another firm introduces a new product, the first firm cuts its price, a third firm introduces a new marketing strategy, and so on. An oligopoly game is a bit like a baseball game with an unlimited number of innings—one firm may come out ahead after one round, but another will emerge on top another day. In the computer industry game, the introduction of personal computers changed the rules. IBM, which had won the mainframe game quite handily, struggles to keep up in a world in which rivals continue to slash prices and improve quality.
Oligopoly games may have more than two players, so the games are more complex, but this does not change their basic structure. The fact that the games are repeated introduces new strategic considerations. A player must consider not just the ways in which its choices will affect its rivals now, but how its choices will affect them in the future as well.
We will keep the game simple, however, and consider a duopoly game. The two firms have colluded, either tacitly or overtly, to create a monopoly solution. As long as each player upholds the agreement, the two firms will earn the maximum economic profit possible in the enterprise.
There will, however, be a powerful incentive for each firm to cheat. The monopoly solution may generate the maximum economic profit possible for the two firms combined, but what if one firm captures some of the other firm’s profit? Suppose, for example, that two equipment rental firms, Quick Rent and Speedy Rent, operate in a community. Given the economies of scale in the business and the size of the community, it is not likely that another firm will enter. Each firm has about half the market, and they have agreed to charge the prices that would be chosen if the two combined as a single firm. Each earns economic profits of $20,000 per month.
Quick and Speedy could cheat on their arrangement in several ways. One of the firms could slash prices, introduce a new line of rental products, or launch an advertising blitz. This approach would not be likely to increase the total profitability of the two firms, but if one firm could take the other by surprise, it might profit at the expense of its rival, at least for a while.
We will focus on the strategy of cutting prices, which we will call a strategy of cheating on the duopoly agreement. The alternative is not to cheat on the agreement. Cheating increases a firm’s profits if its rival does not respond. Figure 11.7 “To Cheat or Not to Cheat: Game Theory in Oligopoly” shows the payoff matrix facing the two firms at a particular time. As in the prisoners’ dilemma matrix, the four cells list the payoffs for the two firms. If neither firm cheats (cell D), profits remain unchanged.
Figure 11.7 To Cheat or Not to Cheat: Game Theory in Oligopoly
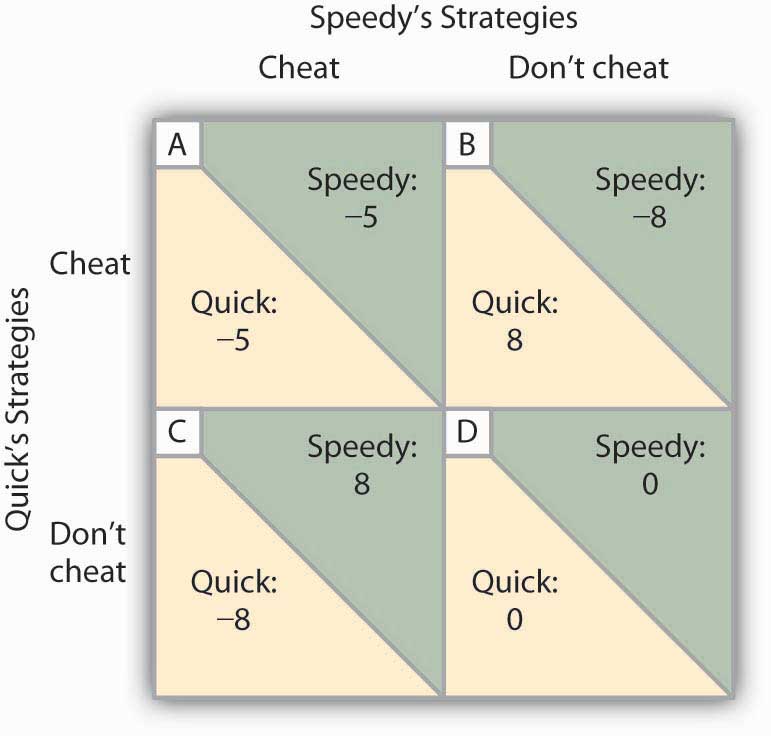
Two rental firms, Quick Rent and Speedy Rent, operate in a duopoly market. They have colluded in the past, achieving a monopoly solution. Cutting prices means cheating on the arrangement; not cheating means maintaining current prices. The payoffs are changes in monthly profits, in thousands of dollars. If neither firm cheats, then neither firm’s profits will change. In this game, cheating is a dominant strategy equilibrium.
This game has a dominant strategy equilibrium. Quick’s preferred strategy, regardless of what Speedy does, is to cheat. Speedy’s best strategy, regardless of what Quick does, is to cheat. The result is that the two firms will select a strategy that lowers their combined profits!
Quick Rent and Speedy Rent face an unpleasant dilemma. They want to maximize profit, yet each is likely to choose a strategy inconsistent with that goal. If they continue the game as it now exists, each will continue to cut prices, eventually driving prices down to the point where price equals average total cost (presumably, the price-cutting will stop there). But that would leave the two firms with zero economic profits.
Both firms have an interest in maintaining the status quo of their collusive agreement. Overt collusion is one device through which the monopoly outcome may be maintained, but that is illegal. One way for the firms to encourage each other not to cheat is to use a tit-for-tat strategy. In a tit-for-tat strategy a firm responds to cheating by cheating, and it responds to cooperative behavior by cooperating. As each firm learns that its rival will respond to cheating by cheating, and to cooperation by cooperating, cheating on agreements becomes less and less likely.
Still another way firms may seek to force rivals to behave cooperatively rather than competitively is to use a trigger strategy , in which a firm makes clear that it is willing and able to respond to cheating by permanently revoking an agreement. A firm might, for example, make a credible threat to cut prices down to the level of average total cost—and leave them there—in response to any price-cutting by a rival. A trigger strategy is calculated to impose huge costs on any firm that cheats—and on the firm that threatens to invoke the trigger. A firm might threaten to invoke a trigger in hopes that the threat will forestall any cheating by its rivals.
Game theory has proved to be an enormously fruitful approach to the analysis of a wide range of problems. Corporations use it to map out strategies and to anticipate rivals’ responses. Governments use it in developing foreign-policy strategies. Military leaders play war games on computers using the basic ideas of game theory. Any situation in which rivals make strategic choices to which competitors will respond can be assessed using game theory analysis.
One rather chilly application of game theory analysis can be found in the period of the Cold War when the United States and the former Soviet Union maintained a nuclear weapons policy that was described by the acronym MAD, which stood for m utually a ssured d estruction. Both countries had enough nuclear weapons to destroy the other several times over, and each threatened to launch sufficient nuclear weapons to destroy the other country if the other country launched a nuclear attack against it or any of its allies. On its face, the MAD doctrine seems, well, mad. It was, after all, a commitment by each nation to respond to any nuclear attack with a counterattack that many scientists expected would end human life on earth. As crazy as it seemed, however, it worked. For 40 years, the two nations did not go to war. While the collapse of the Soviet Union in 1991 ended the need for a MAD doctrine, during the time that the two countries were rivals, MAD was a very effective trigger indeed.
Of course, the ending of the Cold War has not produced the ending of a nuclear threat. Several nations now have nuclear weapons. The threat that Iran will introduce nuclear weapons, given its stated commitment to destroy the state of Israel, suggests that the possibility of nuclear war still haunts the world community.
Key Takeaways
- The key characteristics of oligopoly are a recognition that the actions of one firm will produce a response from rivals and that these responses will affect it. Each firm is uncertain what its rivals’ responses might be.
- The degree to which a few firms dominate an industry can be measured using a concentration ratio or a Herfindahl–Hirschman Index.
- One way to avoid the uncertainty firms face in oligopoly is through collusion. Collusion may be overt, as in the case of a cartel, or tacit, as in the case of price leadership.
- Game theory is a tool that can be used to understand strategic choices by firms.
- Firms can use tit-for-tat and trigger strategies to encourage cooperative behavior by rivals.
Which model of oligopoly would seem to be most appropriate for analyzing firms’ behavior in each of the situations given below?
- When South Airlines lowers its fare between Miami and New York City, North Airlines lowers its fare between the two cities. When South Airlines raises its fare, North Airlines does too.
- Whenever Bank A raises interest rates on car loans, other banks in the area do too.
- In 1986, Saudi Arabia intentionally flooded the market with oil in order to punish fellow OPEC members for cheating on their production quotas.
- In July 1998, Saudi Arabia floated a proposal in which a group of eight or nine major oil-exporting countries (including OPEC members and some nonmembers, such as Mexico) would manage world oil prices by adjusting their production.
Case in Point: Memory Chip Makers Caught in Global Price-Fixing Scheme
Figure 11.8

Tristendomusic – Chips array – CC BY-SA 2.0.
It may have been the remark by T.L. Chang, vice president of the Taiwan-based memory chip manufacturer Mosel-Vitelic that sparked the investigation by the U.S. Department of Justice Antitrust Division. Mr. Chang was quoted in Taiwan’s Commercial Times in May 2002 as admitting to price-fixing meetings held in Asia among the major producers of DRAM, or dynamic random access memory. DRAM is the most common semi-conductor main memory format for storage and retrieval of information that is used in personal computers, mobile phones, digital cameras, MP3 music players, and other electronics products. At those meetings, as well as through emails and telephone conferences, the main manufacturers of DRAM decided not only what prices to charge and how much to make available, but also exchanged information on DRAM sales for the purpose of monitoring and enforcing adherence to the agreed prices. The collusion lasted for three years—from 1999 to 2002. In December 2001, DRAM prices were less than $1.00. By May of 2002, price had risen to the $4 to $5 range.
The companies that were directly injured by the higher chip prices included Dell, Compaq, Hewlett-Packard, Apple, IBM, and Gateway. In the end, though, the purchasers of their products paid in the form of higher prices or less memory.
In December 2003, a Micron Technology sales manager pled guilty to obstruction of justice and served six months of home detention. The first chipmaker to plead guilty a year later was Germany-based Infineon Technologies, which was fined $160 million. As of September 2007, five companies, Samsung being the largest, had been charged fines of more than $732 million, and over 3,000 days of jail time had been meted out to eighteen corporate executives.
The sharp reduction in the number of DRAM makers in the late 1990s undoubtedly made it easier to collude. The industry is still quite concentrated with Samsung holding 27.7% of the market and Hynix 21.3%. The price, however, has fallen quite sharply in recent years.
Sources: Department of Justice, “Sixth Samsung Executive Agrees to Plead Guilty to Participating in DRAM Price-Fixing Cartel,” Press Release April 19, 2007; Stephen Labaton, “Infineon To Pay a Fine in the Fixing of Chip Prices,” The New York Times , September 16, 2004; George Leopold and David Lammers, “DRAMs Under Gun in Antitrust Probe”, Electronic Engineering Times , 1124 (June 24, 2002):1, 102; Lee Sun-Young, “Samsung Cements DRAM Leadership,” Korea Herald , online, March 31, 2008.
Answers to Try It! Problems
- North Airlines seems to be practicing a price strategy known in game theory as tit-for-tat.
- The banks could be engaged in tacit collusion, with Bank A as the price leader.
- Saudi Arabia appears to have used a trigger strategy, another aspect of game theory. In general, of course, participants hope they will never have to “pull” the trigger, because doing so harms all participants. After years of cheating by other OPEC members, Saudi Arabia did undertake a policy that hurt all members of OPEC, including itself; OPEC has never since regained the prominent role it played in oil markets.
- Saudi Arabia seems to be trying to create another oil cartel, a form of overt collusion.
1 One legal cartel is the NCAA, which many economists regard as a successful device through which member firms (colleges and universities) collude on a wide range of rules through which they produce sports.
Principles of Economics Copyright © 2016 by University of Minnesota is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 10. Monopolistic Competition and Oligopoly
10.2 Oligopoly
Learning objectives.
- Explain why and how oligopolies exist
- Contrast collusion and competition
- Interpret and analyze the prisoner’s dilemma diagram
- Evaluate the tradeoffs of imperfect competition
Many purchases that individuals make at the retail level are produced in markets that are neither perfectly competitive, monopolies, nor monopolistically competitive. Rather, they are oligopolies. Oligopoly arises when a small number of large firms have all or most of the sales in an industry. Examples of oligopoly abound and include the auto industry, cable television, and commercial air travel. Oligopolistic firms are like cats in a bag. They can either scratch each other to pieces or cuddle up and get comfortable with one another. If oligopolists compete hard, they may end up acting very much like perfect competitors, driving down costs and leading to zero profits for all. If oligopolists collude with each other, they may effectively act like a monopoly and succeed in pushing up prices and earning consistently high levels of profit. Oligopolies are typically characterized by mutual interdependence where various decisions such as output, price, advertising, and so on, depend on the decisions of the other firm(s). Analyzing the choices of oligopolistic firms about pricing and quantity produced involves considering the pros and cons of competition versus collusion at a given point in time.
Why Do Oligopolies Exist?
A combination of the barriers to entry that create monopolies and the product differentiation that characterizes monopolistic competition can create the setting for an oligopoly. For example, when a government grants a patent for an invention to one firm, it may create a monopoly. When the government grants patents to, for example, three different pharmaceutical companies that each has its own drug for reducing high blood pressure, those three firms may become an oligopoly.
Similarly, a natural monopoly will arise when the quantity demanded in a market is only large enough for a single firm to operate at the minimum of the long-run average cost curve. In such a setting, the market has room for only one firm, because no smaller firm can operate at a low enough average cost to compete, and no larger firm could sell what it produced given the quantity demanded in the market.
Quantity demanded in the market may also be two or three times the quantity needed to produce at the minimum of the average cost curve—which means that the market would have room for only two or three oligopoly firms (and they need not produce differentiated products). Again, smaller firms would have higher average costs and be unable to compete, while additional large firms would produce such a high quantity that they would not be able to sell it at a profitable price. This combination of economies of scale and market demand creates the barrier to entry, which led to the Boeing-Airbus oligopoly for large passenger aircraft.
The product differentiation at the heart of monopolistic competition can also play a role in creating oligopoly. For example, firms may need to reach a certain minimum size before they are able to spend enough on advertising and marketing to create a recognizable brand name. The problem in competing with, say, Coca-Cola or Pepsi is not that producing fizzy drinks is technologically difficult, but rather that creating a brand name and marketing effort to equal Coke or Pepsi is an enormous task.
Collusion or Competition?
When oligopoly firms in a certain market decide what quantity to produce and what price to charge, they face a temptation to act as if they were a monopoly. By acting together, oligopolistic firms can hold down industry output, charge a higher price, and divide up the profit among themselves. When firms act together in this way to reduce output and keep prices high, it is called collusion . A group of firms that have a formal agreement to collude to produce the monopoly output and sell at the monopoly price is called a cartel . See the following Clear It Up feature for a more in-depth analysis of the difference between the two.
Collusion versus cartels: How can I tell which is which?
In the United States, as well as many other countries, it is illegal for firms to collude since collusion is anti-competitive behavior, which is a violation of antitrust law. Both the Antitrust Division of the Justice Department and the Federal Trade Commission have responsibilities for preventing collusion in the United States.
The problem of enforcement is finding hard evidence of collusion. Cartels are formal agreements to collude. Because cartel agreements provide evidence of collusion, they are rare in the United States. Instead, most collusion is tacit, where firms implicitly reach an understanding that competition is bad for profits.
The desire of businesses to avoid competing so that they can instead raise the prices that they charge and earn higher profits has been well understood by economists. Adam Smith wrote in Wealth of Nations in 1776: “People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices.”
Even when oligopolists recognize that they would benefit as a group by acting like a monopoly, each individual oligopoly faces a private temptation to produce just a slightly higher quantity and earn slightly higher profit—while still counting on the other oligopolists to hold down their production and keep prices high. If at least some oligopolists give in to this temptation and start producing more, then the market price will fall. Indeed, a small handful of oligopoly firms may end up competing so fiercely that they all end up earning zero economic profits—as if they were perfect competitors.
The Prisoner’s Dilemma
Because of the complexity of oligopoly, which is the result of mutual interdependence among firms, there is no single, generally-accepted theory of how oligopolies behave, in the same way that we have theories for all the other market structures. Instead, economists use game theory , a branch of mathematics that analyzes situations in which players must make decisions and then receive payoffs based on what other players decide to do. Game theory has found widespread applications in the social sciences, as well as in business, law, and military strategy.
The prisoner’s dilemma is a scenario in which the gains from cooperation are larger than the rewards from pursuing self-interest. It applies well to oligopoly. The story behind the prisoner’s dilemma goes like this:
Two co-conspiratorial criminals are arrested. When they are taken to the police station, they refuse to say anything and are put in separate interrogation rooms. Eventually, a police officer enters the room where Prisoner A is being held and says: “You know what? Your partner in the other room is confessing. So your partner is going to get a light prison sentence of just one year, and because you’re remaining silent, the judge is going to stick you with eight years in prison. Why don’t you get smart? If you confess, too, we’ll cut your jail time down to five years, and your partner will get five years, also.” Over in the next room, another police officer is giving exactly the same speech to Prisoner B. What the police officers do not say is that if both prisoners remain silent, the evidence against them is not especially strong, and the prisoners will end up with only two years in jail each.
The game theory situation facing the two prisoners is shown in Table 3 . To understand the dilemma, first consider the choices from Prisoner A’s point of view. If A believes that B will confess, then A ought to confess, too, so as to not get stuck with the eight years in prison. But if A believes that B will not confess, then A will be tempted to act selfishly and confess, so as to serve only one year. The key point is that A has an incentive to confess regardless of what choice B makes! B faces the same set of choices, and thus will have an incentive to confess regardless of what choice A makes. Confess is considered the dominant strategy or the strategy an individual (or firm) will pursue regardless of the other individual’s (or firm’s) decision. The result is that if prisoners pursue their own self-interest, both are likely to confess, and end up doing a total of 10 years of jail time between them.
| Remain Silent (cooperate with other prisoner) | Confess (do not cooperate with other prisoner) | ||
| Remain Silent (cooperate with other prisoner) | A gets 2 years, B gets 2 years | A gets 8 years, B gets 1 year | |
| Confess (do not cooperate with other prisoner) | A gets 1 year, B gets 8 years | A gets 5 years B gets 5 years | |
| The Prisoner’s Dilemma Problem | |||
The game is called a dilemma because if the two prisoners had cooperated by both remaining silent, they would only have had to serve a total of four years of jail time between them. If the two prisoners can work out some way of cooperating so that neither one will confess, they will both be better off than if they each follow their own individual self-interest, which in this case leads straight into longer jail terms.
The Oligopoly Version of the Prisoner’s Dilemma
The members of an oligopoly can face a prisoner’s dilemma, also. If each of the oligopolists cooperates in holding down output, then high monopoly profits are possible. Each oligopolist, however, must worry that while it is holding down output, other firms are taking advantage of the high price by raising output and earning higher profits. Table 4 shows the prisoner’s dilemma for a two-firm oligopoly—known as a duopoly . If Firms A and B both agree to hold down output, they are acting together as a monopoly and will each earn $1,000 in profits. However, both firms’ dominant strategy is to increase output, in which case each will earn $400 in profits.
| Hold Down Output (cooperate with other firm) | Increase Output (do not cooperate with other firm) | ||
| Hold Down Output (cooperate with other firm) | A gets $1,000, B gets $1,000 | A gets $200, B gets $1,500 | |
| Increase Output (do not cooperate with other firm) | A gets $1,500, B gets $200 | A gets $400, B gets $400 | |
| A Prisoner’s Dilemma for Oligopolists | |||
Can the two firms trust each other? Consider the situation of Firm A:
- If A thinks that B will cheat on their agreement and increase output, then A will increase output, too, because for A the profit of $400 when both firms increase output (the bottom right-hand choice in Table 4 ) is better than a profit of only $200 if A keeps output low and B raises output (the upper right-hand choice in the table).
- If A thinks that B will cooperate by holding down output, then A may seize the opportunity to earn higher profits by raising output. After all, if B is going to hold down output, then A can earn $1,500 in profits by expanding output (the bottom left-hand choice in the table) compared with only $1,000 by holding down output as well (the upper left-hand choice in the table).
Thus, firm A will reason that it makes sense to expand output if B holds down output and that it also makes sense to expand output if B raises output. Again, B faces a parallel set of decisions.
The result of this prisoner’s dilemma is often that even though A and B could make the highest combined profits by cooperating in producing a lower level of output and acting like a monopolist, the two firms may well end up in a situation where they each increase output and earn only $400 each in profits . The following Clear It Up feature discusses one cartel scandal in particular.
What is the Lysine cartel?
Lysine, a $600 million-a-year industry, is an amino acid used by farmers as a feed additive to ensure the proper growth of swine and poultry. The primary U.S. producer of lysine is Archer Daniels Midland (ADM), but several other large European and Japanese firms are also in this market. For a time in the first half of the 1990s, the world’s major lysine producers met together in hotel conference rooms and decided exactly how much each firm would sell and what it would charge. The U.S. Federal Bureau of Investigation (FBI), however, had learned of the cartel and placed wire taps on a number of their phone calls and meetings.
From FBI surveillance tapes, following is a comment that Terry Wilson, president of the corn processing division at ADM, made to the other lysine producers at a 1994 meeting in Mona, Hawaii:
I wanna go back and I wanna say something very simple. If we’re going to trust each other, okay, and if I’m assured that I’m gonna get 67,000 tons by the year’s end, we’re gonna sell it at the prices we agreed to . . . The only thing we need to talk about there because we are gonna get manipulated by these [expletive] buyers—they can be smarter than us if we let them be smarter. . . . They [the customers] are not your friend. They are not my friend. And we gotta have ‘em, but they are not my friends. You are my friend. I wanna be closer to you than I am to any customer. Cause you can make us … money. … And all I wanna tell you again is let’s—let’s put the prices on the board. Let’s all agree that’s what we’re gonna do and then walk out of here and do it.
The price of lysine doubled while the cartel was in effect. Confronted by the FBI tapes, Archer Daniels Midland pled guilty in 1996 and paid a fine of $100 million. A number of top executives, both at ADM and other firms, later paid fines of up to $350,000 and were sentenced to 24–30 months in prison.
In another one of the FBI recordings, the president of Archer Daniels Midland told an executive from another competing firm that ADM had a slogan that, in his words, had “penetrated the whole company.” The company president stated the slogan this way: “Our competitors are our friends. Our customers are the enemy.” That slogan could stand as the motto of cartels everywhere.
How to Enforce Cooperation
How can parties who find themselves in a prisoner’s dilemma situation avoid the undesired outcome and cooperate with each other? The way out of a prisoner’s dilemma is to find a way to penalize those who do not cooperate.
Perhaps the easiest approach for colluding oligopolists, as you might imagine, would be to sign a contract with each other that they will hold output low and keep prices high. If a group of U.S. companies signed such a contract, however, it would be illegal. Certain international organizations, like the nations that are members of the Organization of Petroleum Exporting Countries (OPEC) , have signed international agreements to act like a monopoly, hold down output, and keep prices high so that all of the countries can make high profits from oil exports. Such agreements, however, because they fall in a gray area of international law, are not legally enforceable. If Nigeria, for example, decides to start cutting prices and selling more oil, Saudi Arabia cannot sue Nigeria in court and force it to stop.
Visit the Organization of the Petroleum Exporting Countries website and learn more about its history and how it defines itself.

Because oligopolists cannot sign a legally enforceable contract to act like a monopoly, the firms may instead keep close tabs on what other firms are producing and charging. Alternatively, oligopolists may choose to act in a way that generates pressure on each firm to stick to its agreed quantity of output.
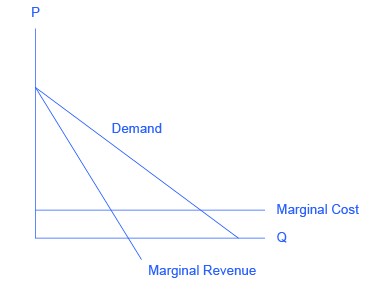
One example of the pressure these firms can exert on one another is the kinked demand curve , in which competing oligopoly firms commit to match price cuts, but not price increases. This situation is shown in Figure 1 . Say that an oligopoly airline has agreed with the rest of a cartel to provide a quantity of 10,000 seats on the New York to Los Angeles route, at a price of $500. This choice defines the kink in the firm’s perceived demand curve. The reason that the firm faces a kink in its demand curve is because of how the other oligopolists react to changes in the firm’s price. If the oligopoly decides to produce more and cut its price, the other members of the cartel will immediately match any price cuts—and therefore, a lower price brings very little increase in quantity sold.
If one firm cuts its price to $300, it will be able to sell only 11,000 seats. However, if the airline seeks to raise prices, the other oligopolists will not raise their prices, and so the firm that raised prices will lose a considerable share of sales. For example, if the firm raises its price to $550, its sales drop to 5,000 seats sold. Thus, if oligopolists always match price cuts by other firms in the cartel, but do not match price increases, then none of the oligopolists will have a strong incentive to change prices, since the potential gains are minimal. This strategy can work like a silent form of cooperation, in which the cartel successfully manages to hold down output, increase price , and share a monopoly level of profits even without any legally enforceable agreement.
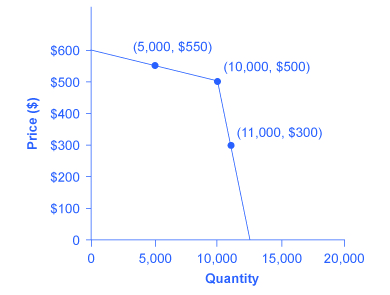
Many real-world oligopolies, prodded by economic changes, legal and political pressures, and the egos of their top executives, go through episodes of cooperation and competition. If oligopolies could sustain cooperation with each other on output and pricing, they could earn profits as if they were a single monopoly. However, each firm in an oligopoly has an incentive to produce more and grab a bigger share of the overall market; when firms start behaving in this way, the market outcome in terms of prices and quantity can be similar to that of a highly competitive market.
Tradeoffs of Imperfect Competition
Monopolistic competition is probably the single most common market structure in the U.S. economy. It provides powerful incentives for innovation, as firms seek to earn profits in the short run, while entry assures that firms do not earn economic profits in the long run. However, monopolistically competitive firms do not produce at the lowest point on their average cost curves. In addition, the endless search to impress consumers through product differentiation may lead to excessive social expenses on advertising and marketing.
Oligopoly is probably the second most common market structure. When oligopolies result from patented innovations or from taking advantage of economies of scale to produce at low average cost, they may provide considerable benefit to consumers. Oligopolies are often buffeted by significant barriers to entry, which enable the oligopolists to earn sustained profits over long periods of time. Oligopolists also do not typically produce at the minimum of their average cost curves. When they lack vibrant competition, they may lack incentives to provide innovative products and high-quality service.
The task of public policy with regard to competition is to sort through these multiple realities, attempting to encourage behavior that is beneficial to the broader society and to discourage behavior that only adds to the profits of a few large companies, with no corresponding benefit to consumers. Monopoly and Antitrust Policy discusses the delicate judgments that go into this task.
The Temptation to Defy the Law
Oligopolistic firms have been called “cats in a bag,” as this chapter mentioned. The French detergent makers chose to “cozy up” with each other. The result? An uneasy and tenuous relationship. When the Wall Street Journal reported on the matter, it wrote: “According to a statement a Henkel manager made to the [French anti-trust] commission, the detergent makers wanted ‘to limit the intensity of the competition between them and clean up the market.’ Nevertheless, by the early 1990s, a price war had broken out among them.” During the soap executives’ meetings, which sometimes lasted more than four hours, complex pricing structures were established. “One [soap] executive recalled ‘chaotic’ meetings as each side tried to work out how the other had bent the rules.” Like many cartels, the soap cartel disintegrated due to the very strong temptation for each member to maximize its own individual profits.
How did this soap opera end? After an investigation, French antitrust authorities fined Colgate-Palmolive, Henkel, and Proctor & Gamble a total of €361 million ($484 million). A similar fate befell the icemakers. Bagged ice is a commodity, a perfect substitute, generally sold in 7- or 22-pound bags. No one cares what label is on the bag. By agreeing to carve up the ice market, control broad geographic swaths of territory, and set prices, the icemakers moved from perfect competition to a monopoly model. After the agreements, each firm was the sole supplier of bagged ice to a region; there were profits in both the long run and the short run. According to the courts: “These companies illegally conspired to manipulate the marketplace.” Fines totaled about $600,000—a steep fine considering a bag of ice sells for under $3 in most parts of the United States.
Even though it is illegal in many parts of the world for firms to set prices and carve up a market, the temptation to earn higher profits makes it extremely tempting to defy the law.
Key Concepts and Summary
An oligopoly is a situation where a few firms sell most or all of the goods in a market. Oligopolists earn their highest profits if they can band together as a cartel and act like a monopolist by reducing output and raising price. Since each member of the oligopoly can benefit individually from expanding output, such collusion often breaks down—especially since explicit collusion is illegal.
The prisoner’s dilemma is an example of game theory. It shows how, in certain situations, all sides can benefit from cooperative behavior rather than self-interested behavior. However, the challenge for the parties is to find ways to encourage cooperative behavior.
Self-Check Questions
- Suppose the firms collude to form a cartel. What price will the cartel charge? What quantity will the cartel supply? How much profit will the cartel earn?
- Suppose now that the cartel breaks up and the oligopolistic firms compete as vigorously as possible by cutting the price and increasing sales. What will the industry quantity and price be? What will the collective profits be of all firms in the industry?
- Compare the equilibrium price, quantity, and profit for the cartel and cutthroat competition outcomes.
| Firm B colludes with Firm A | Firm B cheats by selling more output | |
|---|---|---|
| Firm A colludes with Firm B | A gets $1,000, B gets $100 | A gets $800, B gets $200 |
| Firm A cheats by selling more output | A gets $1,050, B gets $50 | A gets $500, B gets $20 |
Review Questions
- Will the firms in an oligopoly act more like a monopoly or more like competitors? Briefly explain.
- Does each individual in a prisoner’s dilemma benefit more from cooperation or from pursuing self-interest? Explain briefly.
- What stops oligopolists from acting together as a monopolist and earning the highest possible level of profits?
Critical Thinking Questions
- Would you expect the kinked demand curve to be more extreme (like a right angle) or less extreme (like a normal demand curve) if each firm in the cartel produces a near-identical product like OPEC and petroleum? What if each firm produces a somewhat different product? Explain your reasoning.
- When OPEC raised the price of oil dramatically in the mid-1970s, experts said it was unlikely that the cartel could stay together over the long term—that the incentives for individual members to cheat would become too strong. More than forty years later, OPEC still exists. Why do you think OPEC has been able to beat the odds and continue to collude? Hint: You may wish to consider non-economic reasons.
- Mary and Raj are the only two growers who provide organically grown corn to a local grocery store. They know that if they cooperated and produced less corn, they could raise the price of the corn. If they work independently, they will each earn $100. If they decide to work together and both lower their output, they can each earn $150. If one person lowers output and the other does not, the person who lowers output will earn $0 and the other person will capture the entire market and will earn $200. Table 6 represents the choices available to Mary and Raj. What is the best choice for Raj if he is sure that Mary will cooperate? If Mary thinks Raj will cheat, what should Mary do and why? What is the prisoner’s dilemma result? What is the preferred choice if they could ensure cooperation? A = Work independently; B = Cooperate and Lower Output. (Each results entry lists Raj’s earnings first, and Mary’s earnings second.)
| A | B | ||
| A | (30, 30) | (15, 35) | |
| B | (35, 15) | (20, 20) | |
The United States Department of Justice. “Antitrust Division.” Accessed October 17, 2013. http://www.justice.gov/atr/.
eMarketer.com. 2014. “Total US Ad Spending to See Largest Increase Since 2004: Mobile advertising leads growth; will surpass radio, magazines and newspapers this year. Accessed March 12, 2015. http://www.emarketer.com/Article/Total-US-Ad-Spending-See-Largest-Increase-Since-2004/1010982.
Federal Trade Commission. “About the Federal Trade Commission.” Accessed October 17, 2013. http://www.ftc.gov/ftc/about.shtm.
Answers to Self-Check Questions
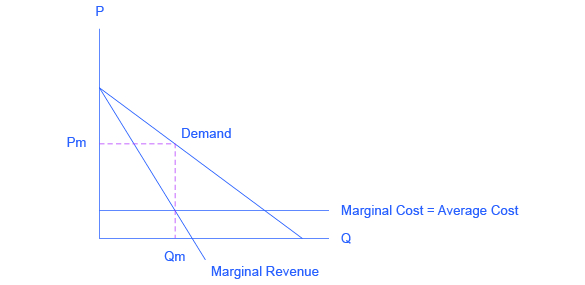
- Pc > Pcc. Qc < Qcc. Profit for the cartel is positive and large. Profit for cutthroat competition is zero.
- Firm B reasons that if it cheats and Firm A does not notice, it will double its money. Since Firm A’s profits will decline substantially, however, it is likely that Firm A will notice and if so, Firm A will cheat also, with the result that Firm B will lose 90% of what it gained by cheating. Firm A will reason that Firm B is unlikely to risk cheating. If neither firm cheats, Firm A earns $1000. If Firm A cheats, assuming Firm B does not cheat, A can boost its profits only a little, since Firm B is so small. If both firms cheat, then Firm A loses at least 50% of what it could have earned. The possibility of a small gain ($50) is probably not enough to induce Firm A to cheat, so in this case it is likely that both firms will collude.
Principles of Economics Copyright © 2016 by Rice University is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

18 Models of Oligopoly: Cournot, Bertrand, and Stackelberg
Cournot, Bertrand, and Stackelberg
The Policy Question How Should the Government Have Responded to Big Oil Company Mergers?
Exploring the policy question.
- How do oil companies compete—on quantities or prices?
- What policy solutions present themselves from this analysis?
Learning Objectives
18.1 cournot model of oligopoly: quantity setters.
Learning Objective 18.1 : Describe how oligopolist firms that choose quantities can be modeled using game theory.
18.2 Bertrand Model of Oligopoly: Price Setters
Learning Objective 18.2 : Describe how oligopolist firms that choose prices can be modeled using game theory.
18.3 Stackelberg Model of Oligopoly: First-Mover Advantage
Learning Objective 18.3 : Describe the different outcomes when oligopolist firms choose quantities sequentially.
18.4 Policy Example How Should the Government Have Responded to Big Oil Company Mergers?
Learning Objective 18.4 : Explain how models of oligopoly can help us understand how to respond to proposed mergers of oil companies that sell retail gas.
Oligopoly markets are markets in which only a few firms compete, where firms produce homogeneous or differentiated products, and where barriers to entry exist that may be natural or constructed. There are three main models of oligopoly markets, and each is considered a slightly different competitive environment. The Cournot model considers firms that make an identical product and make output decisions simultaneously. The Bertrand model considers firms that make an identical product but compete on price and make their pricing decisions simultaneously. The Stackelberg model considers quantity-setting firms with an identical product that make output decisions simultaneously. This chapter considers all three in order, beginning with the Cournot model.
| Number of firms | Similarity of goods | Barriers to entry or exit | Chapter | |
|---|---|---|---|---|
| Perfect competition | Many | Identical | No | |
| Monopolistic competition | Many | Distinct | No | |
| Oligopoly | Few | Identical or distinct | Yes | 18 |
| Monopoly | One | Unique | Yes |
Oligopolists face downward-sloping demand curves, which means that price is a function of the total quantity produced, which, in turn, implies that one firm’s output affects not only the price it receives for its output but the price its competitors receive as well. This creates a strategic environment where one firm’s profit maximizing output level is a function of its competitors’ output levels. The model we use to analyze this is one first introduced by French economist and mathematician Antoine Augustin Cournot in 1838. Interestingly, the solution to the Cournot model is the same as the more general Nash equilibrium concept introduced by John Nash in 1949 and the one used to solve for equilibrium in non-cooperative games in chapter 17 .
We will start by considering the simplest situation: two companies that make an identical product and that have the same cost function. Later we will explore what happens when we relax those assumptions and allow more firms, differentiated products, and different cost functions.
Let’s begin by considering a situation where there are two oil refineries located in the Denver, Colorado, area that are the only two providers of gasoline for the Rocky Mountain regional wholesale market. We’ll call them Federal Gas and National Gas. The gas they produce is identical, and they each decide independently—and without knowing the other’s choice—the quantity of gas to produce for the week at the beginning of each week. We will call Federal’s output choice [latex]q_F[/latex] and National’s output choice [latex]q_N[/latex], where [latex]q[/latex] represents liters of gasoline. The weekly demand for wholesale gas in the Rocky Mountain region is [latex]P=A—BQ[/latex], where [latex]Q[/latex] is the total quantity of gas supplied by the two firms, or [latex]Q=q_F+q_N[/latex]. Immediately, you can see the strategic component: the price they both receive for their gas is a function of each company’s output. We will assume that each liter of gas produced costs the company c, or that c is the marginal cost of producing a liter of gas for both companies and that there are no fixed costs.
If the profit function is [latex]\pi_F[/latex][latex]=[/latex] [latex]q_F(A-B(q_F+q_N)-c)[/latex] , then we can find the optimal output level by solving for the stationary point, or solving
[latex]\frac{\partial \pi_F}{\partial q_F}[/latex] [latex]=[/latex] [latex]_0[/latex]
If [latex]\pi_F=[/latex] [latex]q_F(A-B(q_F+q_N)-c)[/latex] , then we can expand to find
[latex]\pi_F[/latex] [latex]=[/latex][latex]Aq_F-Bq[/latex] [latex]\frac{F}{2}[/latex] [latex]-Bq_Fq_N-cq_F[/latex]
Taking the partial derivative of this expression with respect to [latex]q_F[/latex] ,
[latex]\frac{\partial \pi_F}{\partial q_F}[/latex] [latex]=[/latex][latex]A-2Bq_F-Bq_N-c[/latex] [latex]=[/latex] [latex]_0[/latex]
If we rearrange this, we can see that this is simply an expression of [latex]MR=MC[/latex] .
[latex]A-2Bq_F-Bq_N[/latex][latex]=[/latex][latex]c[/latex]
The marginal revenue looks the same as a monopolist’s [latex]MR[/latex] function but with one additional term, [latex]-[/latex] [latex]Bq_N[/latex] .
Solving for [latex]q_F[/latex] yields
[latex]q_F=[/latex] [latex]\frac{A-Bq_N-c}{2B}[/latex] ,
[latex]q^*_F=[/latex] [latex]\frac{A-c}{2B}-\frac{1}{2}[/latex] [latex]qN[/latex]
This is Federal Gas’s best response function, their profit maximizing output level given the output choice of their rivals. It is the same best response function as the ones in chapter 17 . By symmetry, National Gas has an identical best response function:
[latex]q^*_N=[/latex] [latex]\frac{A-c}{2B}-\frac{1}{2}[/latex] [latex]qF[/latex]
With these assumptions in place, we can express Federal’s profit function:
[latex]\pi_F=P \times q_F—c \times q_F = q_F (P-c)[/latex]
Substituting the inverse demand curve, we arrive at the expression
[latex]\pi_F=q_F(A-BQ-c)[/latex].
Substituting [latex]Q=q_A+q_B[/latex] yields
[latex]\pi_F=q_F(A-B(q_F+q_N)-c)[/latex].
The expression for National is symmetric:
[latex]\pi_N=q_N(A-B(q_N+q_F)-c)[/latex]
Note that we have now described a game complete with players, Federal and National; strategies, [latex]q_F[/latex] and [latex]q_N[/latex]; and payoffs, [latex]\pi_F[/latex] and [latex]\pi_N[/latex]. Now the task is to search for the equilibrium of the game. To do so, we have to begin with a best response function. In this case, the best response is the firm’s profit maximizing output. This will depend on both the firm’s own output and the competing firm’s output.
We know from chapter 15 that the monopolists’ marginal revenue curve when facing an inverse demand curve [latex]P=A-BQ[/latex] is [latex]MR(q)=A-2Bq[/latex]. This duopolistic example shows that the firms’ marginal revenue curves include one extra term:
[latex]MR_F(q_F)=A-2Bq_F-Bq_N[/latex] and [latex]MR_N(q_N)=A-2Bq_N-Bq_F[/latex]
The profit maximizing rule tells us that to find the profit maximizing output, we must set the marginal revenue to the marginal cost and solve. Doing so yields
[latex]q^*_F=\frac{A-c}{2B}-\frac{1}{2}qN[/latex]
for Federal Gas and
[latex]q^*_N=\frac{A-c}{2B}-\frac{1}{2}qF[/latex]
for National Gas. These are the firms’ best response functions, their profit maximizing output levels given the output choice of their rivals.
Now that we know the best response functions, solving for equilibrium in the model is relatively straightforward. We can begin by graphing the best response functions. These graphical illustrations of the best response functions are called reaction curves. A Nash equilibrium is a correspondence of best response functions, which is the same as a crossing of the reaction curves.
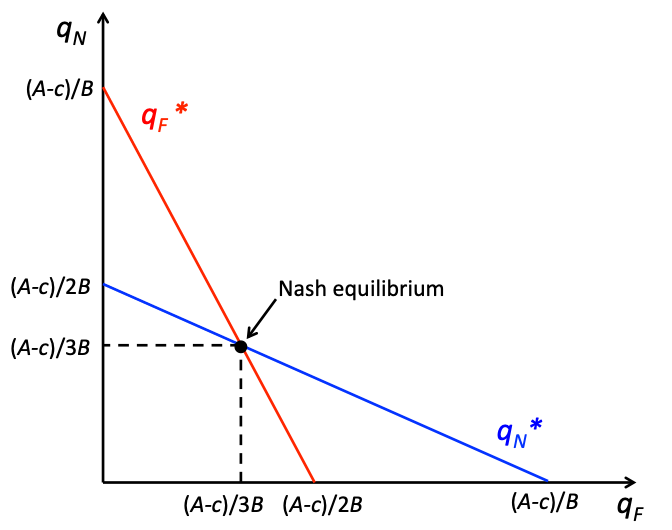
In figure 18.1 , we can see the Nash equilibrium of the Cournot duopoly model as the intersection of the reaction curves. Mathematically, this intersection is found by simultaneously solving
[latex]q^*_F=\frac{A-c}{2B}-\frac{1}{2}q_N[/latex] and [latex]q^*_F=\frac{A-c}{2B}-\frac{1}{2}q_F[/latex]
This is a system of two equations and two unknowns and therefore has a unique solution as long as the slopes are not equal. We can solve these by substituting one equation into the other, which yields a single equation with a single unknown:
[latex]q^*_F=\frac{A-c}{2B}-\frac{1}{2}[\frac{A-c}{2B}-\frac{1}{2}q_F][/latex]
Solving this by steps results in the following:
[latex]q^*_F=\frac{A-c}{2B}-\frac{A-c}{4B}+\frac{1}{4}q_F[/latex][latex]\frac{3}{4}q^*_F=\frac{A-c}{4B}[/latex] [latex]q^*_F=\frac{A-c}{3B}[/latex]
And by symmetry, we know that the two optimal quantities are the same:
[latex]q^*_N=\frac{A-c}{3B}[/latex]
The Nash equilibrium is
[latex](q^*_F,q^*_N)[/latex]
[latex](\frac{A-c}{3B}, \frac{A-c}{3B})[/latex].
Let’s consider a specific example. Suppose in the above example, the weekly demand curve for wholesale gas in the Rocky Mountain region is
[latex]p = 1,000 − 2Q[/latex], in thousands of gallons
Both firms have constant marginal costs of 400. In this case,
[latex]A = 1,000[/latex], [latex]B = 2[/latex] and [latex]C = 400[/latex].
[latex]q^*_F=\frac{A-c}{3B}=\frac{1,000 − 400}{(3)(2)}=\frac{600}{6}=100[/latex]
By symmetry, we know
[latex]q^*_N=100[/latex]
as well. So both Federal Gas and National Gas produce 100,000 gallons of gasoline a week. Total output is the sum of the two and is 200,000 gallons. The price is [latex]p= 1,000 − 2(200) = $600[/latex] for 1,000 gallons of gas, or $0.60 a gallon.
To analyze this from the beginning, we can set up the total revenue function for Federal Gas:
[latex]TR(q_F)=p×q_F[/latex] [latex]=(1,000 − 2Q)q_F[/latex] [latex]=(1,000 − 2q_F-2q_N)q_F[/latex] [latex]= 1,000 − 2q \frac{2}{F}-2q_Fq_N[/latex]
The marginal revenue function that is associated with this is
[latex]MR(q_F)=1,000 − 4q_F-2q_N[/latex].
We know marginal cost is 400, so setting marginal revenue equal to marginal cost results in the following expression:
[latex]1,000 − 4q_F-2q_N=400[/latex]
Solving for [latex]q_F[/latex] results in the following:
[latex]q_F=\frac{600 − 2q_N}{4}[/latex] [latex]q^*_F=150-\frac{q_F}{2}[/latex]
This is the best response function for Federal Gas. By symmetry, we know that National Gas has the same best response function:
[latex]q^*_N=150-\frac{q_F}{2}[/latex]
Solving for the Nash equilibrium, we get the following:
[latex]q^*_N=150-\frac{q_F}{2}[/latex] [latex]q^*_F=150 − 75+\frac{q_F}{4}[/latex] [latex]/frac{3}{4}q^*_F=25[/latex] [latex]q^*_F=100[/latex]
We can insert the solution for [latex]q_F[/latex] into [latex]q^*_N[/latex]:
[latex]q^*_N=150-\frac{(100)}{2}=100[/latex]
In the previous section, we studied oligopolists that make an identical good and who compete by setting quantities. The example we used in that section was wholesale gasoline, where the market sets a price that equates supply and demand and the strategic decision of the refiners was how much oil to refine into gasoline. In this section, we turn our attention to a different situation in which the oligopolists compete on price. The example here is the retail gas stations that bought the wholesale gas from the refiners and are now ready to sell it to consumers. We still have identical goods; for consumers, the gas that goes into their cars is all the same, and we will assume away any other differences like cleaner stations or the presence of a mini-mart.
Let’s imagine a simple situation where there are two gas stations, Fast Gas and Speedy Gas, on either side of a busy main street. Both stations have large signs that display the gas prices that each station is offering for the day. Consumers are assumed to be indifferent about the gas or the stations, so they will go to the station that is offering the lower price. So an individual gas station’s demand is conditional on its relative price with the other station.
Formally, we can express this with the following demand function for Fast Gas:
[latex]Q_F \left\{\begin{matrix} & & & \\ a-bP_F \text{ if }P_F P_F \end{matrix}\right.[/latex]
Speedy Gas has an equivalent demand curve:
[latex]Q_S \left\{\begin{matrix} & & & \\ a-bP_S \text{ if }P_S P_F \end{matrix}\right.[/latex]
In other words, these demand curves say that if a station has a lower price than the other, they will get all the demand at that price, and the other station will get no demand. If they have the same price, then each will get one-half of the demand at that price.
Let’s assume that Fast Gas and Speedy Gas both have the same constant marginal cost of [latex]c[/latex] and no fixed costs to keep the analysis simple. The question we now have to answer is, What are the best response functions for the two stations? Remember that best response functions are one player’s optimal strategy choice given the strategy choice of the other player. So what is Fast Gas’s best response to Speedy Gas’s price?
If Speedy Gas charges
[latex]P_S \gt c[/latex]
Fast Gas can set [latex]P_F \gt P_S[/latex] and they will get no customers at all and make a profit of zero. Fast Gas could instead set
[latex]P_F=P_S[/latex]
and get [latex]\frac{1}{2}[/latex] the demand at that price and make a positive profit. Or they could set
[latex]P_F=P_S −$0.01[/latex]
or set their price one cent below Speedy Gas’s price and get all the customers at a price that is one cent below the price, at which they would get [latex]\frac{1}{2}[/latex] the demand.
Clearly, this third option is the one that yields the most profit. Now we just have to consider the case where [latex]P_S=c[/latex]. In this case, undercutting the price by one cent is not optimal because Fast Gas would get all the demand but would lose money on every gallon of gas sold, yielding negative profits. Setting
[latex]P_F=P_S=c[/latex]
would give them half the demand at a break-even price and would yield exactly zero profits.
The best response function we just described for Fast Gas is the same best response function for Speedy Gas. So where are the correspondences of best response functions? As long as the prices are above [latex]c[/latex], there is always an incentive for both stations to undercut each other’s price, so there is no equilibrium. But at [latex]P_F=P_S=c[/latex], both stations are playing their best response to each other simultaneously. So the unique Nash equilibrium to this game is
[latex]P_F=P_S=c[/latex].
What is particularly interesting about this is the fact that this is the same outcome that would have occurred if they were in a perfectly competitive market because competition would have driven prices down to marginal cost. So in a situation where competition is based on price and the good is relatively homogeneous, as few as two firms can drive the market to an efficient outcome.
Both the Cournot model and the Bertrand model assume simultaneous move games. This makes sense when one firm has to make a strategic decision before knowing about the strategy choice of the other firm. But not all situations are like this. What happens when one firm makes its strategic decision first and the other firm chooses second? This is the situation described by the Stackelberg model, where the firms are quantity setters selling homogenous goods.
Let’s return to the example of two oil companies: Federal Gas and National Gas. The gas they produce is identical, but now they decide their output levels sequentially. We will assume that Federal Gas sets its output first, and then after observing Federal’s choice, National Gas decides on the quantity of gas they are going to produce for the week. We will again call Federal’s output choice [latex]q_F[/latex] and National’s output choice [latex]q_N[/latex], where [latex]q[/latex] represents liters of gasoline. The weekly demand for wholesale gas is still [latex]P = A—BQ[/latex], where [latex]Q[/latex] is the total quantity of gas supplied by the two firms, or
[latex]Q=q_F+q_N[/latex].
We have now turned the previous Cournot game into a sequential game, and the [latex]SPNE[/latex] solution to a sequential game is found through backward induction. So we have to start at the second move of the game: National’s output choice. When National makes this decision, Federal’s output choices are already made and known to National, so it is taken as given. Therefore, we can express Federal’s profit function as
[latex]\Pi _N=q_N(A-B(q_N+q_F)-c)[/latex].
This is the same as in the Cournot example, and for National, the best response function is also the same. This is because in the Cournot case, both firms took the other’s output as given.
[latex]q^*_N=\frac{A-c}{2B}-\frac{1}{2}q_F[/latex]
When it comes to Federal’s decision, we diverge from the Cournot model because instead of taking [latex]q_N[/latex] as a given, Federal knows exactly how National will respond because they know the best response function. Federal’s profit function,
[latex]\Pi _F=q_F(A-Bq_F-Bq_N-c)[/latex],
can be re-written, replacing [latex]q_N[/latex] with the best response function:
[latex]\Pi _F=q_F(A-Bq_F-B(\frac{A-C}{2B}-\frac{1}{2})-c)[/latex]
If the profit function is [latex]\Pi_F[/latex] [latex]=[/latex] [latex]q_F([/latex] [latex]\frac{A-C}{2}-[/latex] [latex]B[/latex] [latex]\frac{1}{2}[/latex] [latex]q_F)[/latex] , then we can find the optimal output level by solving for the stationary point, or solving
[latex]\frac{\partial \Pi _F}{\partial q_F}[/latex] [latex]=[/latex] [latex]_0[/latex]
If [latex]\Pi_F[/latex] [latex]=[/latex] [latex]q_F([/latex] [latex]\frac{A-c}{2}-[/latex] [latex]B[/latex] [latex]\frac{1}{2}[/latex] [latex]q_F)[/latex] , then we can expand to find
[latex]\Pi_F[/latex] [latex]=[/latex] [latex]q_F([/latex] [latex]\frac{A-c}{2}[/latex] [latex])q_F[/latex] [latex]-B[/latex] [latex]\frac{1}{2}[/latex] [latex]q_{F}^{2}[/latex]
Taking the partial derivative of this expression with respect to [latex]q_F[/latex], we get
[latex]\frac{\partial \Pi _F}{\partial q_F}[/latex] [latex]=([/latex] [latex]\frac{A-c}{2}[/latex] [latex])[/latex][latex]-[/latex] [latex]Bq_F=[/latex] [latex]_0[/latex]
[latex]q_F=[/latex] [latex]\frac{A-c}{2B}[/latex]
This is Federal Gas’s profit maximizing output level, given that they choose first and can anticipate National’s response.
We can see that Federal’s profits are determined only by their own output once we explicitly consider National’s response. Simplifying yields
[latex]\Pi _F=q_F(\frac{A-c}{2}-B\frac{1}{2}q_F)[/latex].
We know that the second mover’s best response is the same as in section 18.1 , and the solution to the profit optimization problem above yields the following best response function for Federal Gas:
[latex]q^*_F=\frac{A-c}{2B}[/latex],
substituting this into National’s best response function and solving the following:
[latex]q^*_N=\frac{A-c}{2B}-\frac{1}{2}\left [ \frac{A-c}{2B} \right ][/latex]
[latex]q^*_N=\frac{A-c}{2B}-\left [\frac{A-c}{4B} \right][/latex]
[latex]q^*_N=\frac{A-c}{4B}[/latex]
The subgame perfect Nash equilibrium is
([latex]q^*_F[/latex], [latex]q^*_F[/latex])
A few things are worth noting when comparing this outcome to the Nash equilibrium outcome of the Cournot game in section 18.1 . First, the individual output level for Federal, the first mover in the Stackelberg game, the Stackelberg leader , is higher than it is in the Cournot game. Second, the individual output level for National, the second mover in the Stackelberg game, the Stackelberg follower , is lower than it is in the Cournot game. Third, the total output is larger in the Stackelberg outcome than in the Cournot outcome. This means the price is lower because the demand curve is downward sloping. Since the Cournot outcome is one of the options for the Stackelberg leader—if it chooses the same output as in the Cournot case, the follower will as well—it must be true that profits are higher for the Stackelberg leader. And since both the quantity produced and the price received are lower for the Stackelberg follower compared to the Cournot outcome, the profits must be lower as well.
So from this we see the major differences in the Stackelberg model compared to the Cournot model. There is a considerable first-mover advantage . By being able to set its quantity first, Federal Gas is able to gain a larger share of the market for itself, and even though it leads to a lower price, it makes up for that lower price with the increase in quantity to achieve higher profits. The opposite is true for the second mover: by being forced to choose after the leader has set its output, the follower is forced to accept a lower price and lower output. From the consumer’s perspective, the Stackelberg outcome is preferable because overall, there is more quantity at a lower price.
The end of the twentieth century saw a number of mergers of massive oil companies. In 1999, BP Amoco acquired ARCO, followed soon thereafter by Exxon’s acquisition of Mobil. Then, in 2001, Chevron acquired Texaco for $38.7 billion. The newly combined company became the world’s fourth-largest producer of oil and natural gas. Whenever any such mergers and acquisitions are proposed, the US government has to approve the deal, and sometimes this approval comes with conditions designed to protect US consumers from undue harm that the consolidation might cause due to market concentration. In this case, the Federal Trade Commission (FTC) was the agency that provided oversight, and in the end, they approved the merger with the following condition: they had to sell their stake in two massive oil refineries. However, they were largely allowed to retain their retail gas operations, even though both companies had significant market presence and their merger would cause a drop in the competitiveness of the retail gas market, particularly in some areas where both companies had a significant market share.
On their face, these decisions seem to make little sense. How is it that the US government is worried about the impact of the merger on refining and the wholesale gas market but not on the retail gas market? The answer lies in the way these two markets fit into the economic models of oligopoly. Refining and wholesale gas operations are more akin to the Cournot model, where a few firms produce a homogenous product and compete on quantity and the sum total of all gas refined sets the wholesale market price. The insight of the Cournot model is that every merger produces fewer firms, and this constrains supply and increases price. Remember that this is a function not of capacity—that has not changed—but of the strategic environment, which makes it easier for all firms to constrict supply, which, in turn, raises prices and profits. The lower supply and higher prices do material harm to consumers, however, and it is for this reason that the FTC stepped in and demanded that the merged company sell off its interest in two big refining operations.
On the other hand, retail gas is more akin to the Bertrand model, where a bunch of retailers are selling a homogenous good but are competing mostly on price. A cursory examination of the retail gas industry confirms this: prices are posted prominently, and consumers show very strong responses to lower prices. The Bertrand model shows us that it takes very little competition to result in highly competitive pricing, so a merger that might reduce the number of competing gas station brands by one is unlikely to have much of a material effect on prices and therefore will be unlikely to harm consumers.
Viewed through the lens of the models of oligopoly studied in this chapter, the FTC’s decision to demand a divestment in oil refining and wholesale gas operations but mostly allow the retail side to consolidate makes sense. It is no surprise that these are the very same models the government uses to analyze such situations and devise a response.
- Do you think it is correct that wholesale gas looks more like the Cournot model and retail gas looks more like the Bertrand model?
- Do you think the government did the right thing in the case of the Chevron-Texaco merger?
Review: Topics and Related Learning Outcomes
Learn: key topics.
Oligopoly markets are markets in which only a few firms compete, where firms produce homogeneous or differentiated products, and where barriers to entry exist that may be natural or constructed.
The Cournot model considers firms that make an identical product and make output decisions simultaneously.
The Bertrand model considers firms that make an identical product but compete on price and make their pricing decisions simultaneously.
The Stackelberg model considers quantity-setting firms with an identical product that make output decisions simultaneously.
Tables and Graphs

Media Attributions
- 18.1.1 © Patrick M. Emerson is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
Intermediate Microeconomics Copyright © 2019 by Patrick M. Emerson is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
This website uses cookies to ensure you get the best experience on our website. Without cookies your experience may not be seamless.

- The Emergence of Oligopoly: Sugar Refining as a Case Study
In this Book

- Alfred S. Eichner
- Published by: Johns Hopkins University Press
- Funder: Mellon/NEH / Hopkins Open Publishing: Encore Editions
- View Citation

Table of Contents

- New Copyright
- Half Title Page
- 1 • The Larger Framework
- 2 • The Emergence of a Competitive Industry
- 3 • Competition and Instability
- 4 • The Trust is Born
- 5 • Why Consolidation
- 6 • A Change in Legal Form
- pp. 120-151
- 7 • Culmination and Condonation
- pp. 152-187
- 8 • The Problem of Entry
- pp. 188-228
- 9 • The Exercise of Control
- pp. 229-263
- 10 • The Old Order Passeth
- pp. 264-290
- 11 • The Acceptance of Oligopoly
- pp. 291-331
- 12 • Historical Perspectives
- pp. 332-335
- Appendixes and Bibliography
- A • Sugar Refineries Located in New York City, 1868–87
- B • Sugar Refineries Located in Philadelphia, 1869–87
- C • Sugar Refineries Located in Boston, 1868–87
- D • Average Prices of Raw and Refined Sugar for Selected Years, and the Margin between Them
- E • Domestic Sugar-Market Shares
- F • Havemeyer and American Sugar Refining Company Holdings in Sugar Beet Companies, 1907
- pp. 345-349
- Bibliography
- pp. 351-364
- pp. 365-388
Additional Information

Project MUSE Mission
Project MUSE promotes the creation and dissemination of essential humanities and social science resources through collaboration with libraries, publishers, and scholars worldwide. Forged from a partnership between a university press and a library, Project MUSE is a trusted part of the academic and scholarly community it serves.

2715 North Charles Street Baltimore, Maryland, USA 21218
+1 (410) 516-6989 [email protected]
©2024 Project MUSE. Produced by Johns Hopkins University Press in collaboration with The Sheridan Libraries.
Now and Always, The Trusted Content Your Research Requires

Built on the Johns Hopkins University Campus
Reference Library
Collections
- See what's new
- All Resources
- Student Resources
- Assessment Resources
- Teaching Resources
- CPD Courses
- Livestreams
Study notes, videos, interactive activities and more!
Economics news, insights and enrichment
Currated collections of free resources
Browse resources by topic
- All Economics Resources
Resource Selections
Currated lists of resources
- Online Lessons
Oligopoly (Online Lesson)
Last updated 20 Jul 2020
- Share on Facebook
- Share on Twitter
- Share by Email
In this online lesson, we cover the oligopoly market structure.
WHAT YOU'LL STUDY IN THIS ONLINE LESSON
- the characteristics of an oligopoly market structure
- the construction of a kinked demand curve
- price and non-price competition
- the existence of collusion and cartels
- how game theory impacts on the behaviours of oligopolistic firms
Additional teacher guidance is available at the end of this online lesson.
HOW TO USE THIS ONLINE LESSON
Follow along in order of the activities shown below. Some are interactive game-based activities, designed to test your understanding and application of oligopoly. Others are based on short videos, including activities for you to think about and try at home, as well as some extra worksheet-based activities.
If you would like to download a simple PDF worksheet to accompany the video activities, you can find it here . You can print it off and annotate it for your own notes, or make your own notes on a separate piece of paper to add to your school/college file.
ACTIVITY 1: VIDEO - KEY CONCEPTS
In this video, we look at the key concepts that are required when considering the oligopoly market structure including its characteristics and and some real world examples.
ACTIVITY 2: VIDEO - THE KINKED DEMAND CURVE
Kinked demand curve theory is used to explain some of the behaviours of firms that exist in an oligopolistic market. This video discusses how the kinked demand curve is constructed and how it illustrates non-price competition.
ACTIVITY 3: VIDEO - PRICE AND NON-PRICE COMPETITION
This video explained how firms in an oligopolistic market compete with one another and provides some real world examples of non-price competition in action!
ACTIVITY 4: VIDEO - CARTELS AND COLLUSION
The existence of price rigidity in an oligopolistic market can encourage firms to collude. This video examines the causes of business collusion, the creation of cartels and how this can be represented diagrammatically.
ACTIVITY 5: VIDEO - GAME THEORY
This video examines how economists use game theory to model the behaviour of businesses in concentrated markets.
ACTIVITY 6: GAME - TAKEOVERS
Challenge yourself with this short interactive quiz where you have 60 seconds to match the 8 real-world examples of takeovers in concentrated markets.
ACTIVITY 7: GAME - FIRMS THAT EXIST IN OLIGOPOLY MARKETS
Have a go at this 'concentration' activity where you need to match 6 pairs of firms that exist in the same oligpolistic market.
EXTENSION TASKS
- Read this article from the Economist on cartels on Mexico. Identify the reforms put in place by the Mexican government and explain how these might reduce collusive behaviour.
- Read this article from the Economist on Organisation of Petroleum Exporting Countries (OPEC) . Use a cost and revenue diagram to analyse the impact of OPEC’s production cut on the cartel’s profits.
ADDITIONAL TEACHER GUIDANCE
This lesson comprises:
- around 30 minutes of guided video content, spread across 4 videos
- around 15-20 minutes of student thinking and activity time throughout the videos
- 2 interactive games, designed to build awareness of real-world economics and application
- an additional task reviewing the global examples of cartels and collusion.
Follow up this lesson by trying the online lesson on Contestable Markets .
- Tacit Collusion
You might also like
Revenues and profits in the uk cinema industry.
Study Notes

Legal Collusion between Businesses

Neuroscience, game theory, monkeys
30th July 2015
Tesco scales back 24 hour opening in over 70 stores
29th January 2016

Should BT be broken up to stimulate competition?
26th February 2016
Economists advise the football clubs! The failure of UEFA's Financial Fair Play regulations
9th September 2016
Deutsche fined again over LIBOR rigging
26th October 2017
Climate change battle requires international cooperation
18th January 2019
Our subjects
- › Criminology
- › Economics
- › Geography
- › Health & Social Care
- › Psychology
- › Sociology
- › Teaching & learning resources
- › Student revision workshops
- › Online student courses
- › CPD for teachers
- › Livestreams
- › Teaching jobs
Boston House, 214 High Street, Boston Spa, West Yorkshire, LS23 6AD Tel: 01937 848885
- › Contact us
- › Terms of use
- › Privacy & cookies
© 2002-2024 Tutor2u Limited. Company Reg no: 04489574. VAT reg no 816865400.
10.2 Oligopoly
Learning objectives.
By the end of this section, you will be able to:
- Explain why and how oligopolies exist
- Contrast collusion and competition
- Interpret and analyze the prisoner’s dilemma diagram
- Evaluate the tradeoffs of imperfect competition
Many purchases that individuals make at the retail level are produced in markets that are neither perfectly competitive, monopolies, nor monopolistically competitive. Rather, they are oligopolies. Oligopoly arises when a small number of large firms have all or most of the sales in an industry. Examples of oligopoly abound and include the auto industry, cable television, and commercial air travel. Oligopolistic firms are like cats in a bag. They can either scratch each other to pieces or cuddle up and get comfortable with one another. If oligopolists compete hard, they may end up acting very much like perfect competitors, driving down costs and leading to zero profits for all. If oligopolists collude with each other, they may effectively act like a monopoly and succeed in pushing up prices and earning consistently high levels of profit. We typically characterize oligopolies by mutual interdependence where various decisions such as output, price, and advertising depend on other firm(s)' decisions. Analyzing the choices of oligopolistic firms about pricing and quantity produced involves considering the pros and cons of competition versus collusion at a given point in time.
Why Do Oligopolies Exist?
A combination of the barriers to entry that create monopolies and the product differentiation that characterizes monopolistic competition can create the setting for an oligopoly. For example, when a government grants a patent for an invention to one firm, it may create a monopoly. When the government grants patents to, for example, three different pharmaceutical companies that each has its own drug for reducing high blood pressure, those three firms may become an oligopoly.
Similarly, a natural monopoly will arise when the quantity demanded in a market is only large enough for a single firm to operate at the minimum of the long-run average cost curve. In such a setting, the market has room for only one firm, because no smaller firm can operate at a low enough average cost to compete, and no larger firm could sell what it produced given the quantity demanded in the market.
Quantity demanded in the market may also be two or three times the quantity needed to produce at the minimum of the average cost curve—which means that the market would have room for only two or three oligopoly firms (and they need not produce differentiated products). Again, smaller firms would have higher average costs and be unable to compete, while additional large firms would produce such a high quantity that they would not be able to sell it at a profitable price. This combination of economies of scale and market demand creates the barrier to entry, which led to the Boeing-Airbus oligopoly (also called a duopoly) for large passenger aircraft.
The product differentiation at the heart of monopolistic competition can also play a role in creating oligopoly. For example, firms may need to reach a certain minimum size before they are able to spend enough on advertising and marketing to create a recognizable brand name. The problem in competing with, say, Coca-Cola or Pepsi is not that producing fizzy drinks is technologically difficult, but rather that creating a brand name and marketing effort to equal Coke or Pepsi is an enormous task.
Collusion or Competition?
When oligopoly firms in a certain market decide what quantity to produce and what price to charge, they face a temptation to act as if they were a monopoly. By acting together, oligopolistic firms can hold down industry output, charge a higher price, and divide the profit among themselves. When firms act together in this way to reduce output and keep prices high, it is called collusion . A group of firms that have a formal agreement to collude to produce the monopoly output and sell at the monopoly price is called a cartel . See the following Clear It Up feature for a more in-depth analysis of the difference between the two.
Clear It Up
Collusion versus cartels: how to differentiate.
In the United States, as well as many other countries, it is illegal for firms to collude since collusion is anti-competitive behavior, which is a violation of antitrust law. Both the Antitrust Division of the Justice Department and the Federal Trade Commission have responsibilities for preventing collusion in the United States.
The problem of enforcement is finding hard evidence of collusion. Cartels are formal agreements to collude. Because cartel agreements provide evidence of collusion, they are rare in the United States. Instead, most collusion is tacit, where firms implicitly reach an understanding that competition is bad for profits.
Economists have understood for a long time the desire of businesses to avoid competing so that they can instead raise the prices that they charge and earn higher profits. Adam Smith wrote in Wealth of Nations in 1776: “People of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the public, or in some contrivance to raise prices.”
Even when oligopolists recognize that they would benefit as a group by acting like a monopoly, each individual oligopoly faces a private temptation to produce just a slightly higher quantity and earn slightly higher profit—while still counting on the other oligopolists to hold down their production and keep prices high. If at least some oligopolists give in to this temptation and start producing more, then the market price will fall. A small handful of oligopoly firms may end up competing so fiercely that they all find themselves earning zero economic profits—as if they were perfect competitors.
The Prisoner’s Dilemma
Because of the complexity of oligopoly, which is the result of mutual interdependence among firms, there is no single, generally-accepted theory of how oligopolies behave, in the same way that we have theories for all the other market structures. Instead, economists use game theory , a branch of mathematics that analyzes situations in which players must make decisions and then receive payoffs based on what other players decide to do. Game theory has found widespread applications in the social sciences, as well as in business, law, and military strategy.
The prisoner’s dilemma is a scenario in which the gains from cooperation are larger than the rewards from pursuing self-interest. It applies well to oligopoly. (Note that the term "prisoner" is not typically an accurate term for someone who has recently been arrested, but we will use the term here, since this scenario is widely used and referenced in economic, business, and social contexts.) The story behind the prisoner’s dilemma goes like this:
Two co-conspirators are arrested. When they are taken to the police station, they refuse to say anything and are put in separate interrogation rooms. Eventually, a police officer enters the room where Prisoner A is being held and says: “You know what? Your partner in the other room is confessing. Your partner is going to get a light prison sentence of just one year, and because you’re remaining silent, the judge is going to stick you with eight years in prison. Why don’t you get smart? If you confess, too, we’ll cut your jail time down to five years, and your partner will get five years, also.” Over in the next room, another police officer is giving exactly the same speech to Prisoner B. What the police officers do not say is that if both prisoners remain silent, the evidence against them is not especially strong, and the prisoners will end up with only two years in jail each.
The game theory situation facing the two prisoners is in Table 10.2 . To understand the dilemma, first consider the choices from Prisoner A’s point of view. If A believes that B will confess, then A should confess, too, so as to not get stuck with the eight years in prison. However, if A believes that B will not confess, then A will be tempted to act selfishly and confess, so as to serve only one year. The key point is that A has an incentive to confess regardless of what choice B makes! B faces the same set of choices, and thus will have an incentive to confess regardless of what choice A makes. To confess is called the dominant strategy. It is the strategy an individual (or firm) will pursue regardless of the other individual’s (or firm’s) decision. The result is that if prisoners pursue their own self-interest, both are likely to confess, and end up being sentenced to a total of 10 years of jail time between them.
| Remain Silent (cooperate with other prisoner) | Confess (do not cooperate with other prisoner) | ||
| Remain Silent (cooperate with other prisoner) | A gets 2 years, B gets 2 years | A gets 8 years, B gets 1 year | |
| Confess (do not cooperate with other prisoner) | A gets 1 year, B gets 8 years | A gets 5 years B gets 5 years | |
The game is called a dilemma because if the two prisoners had cooperated by both remaining silent, they would only have been incarcerated for two years each, for a total of four years between them. If the two prisoners can work out some way of cooperating so that neither one will confess, they will both be better off than if they each follow their own individual self-interest, which in this case leads straight into longer terms.
The Oligopoly Version of the Prisoner’s Dilemma
The members of an oligopoly can face a prisoner’s dilemma, also. If each of the oligopolists cooperates in holding down output, then high monopoly profits are possible. Each oligopolist, however, must worry that while it is holding down output, other firms are taking advantage of the high price by raising output and earning higher profits. Table 10.3 shows the prisoner’s dilemma for a two-firm oligopoly—known as a duopoly . If Firms A and B both agree to hold down output, they are acting together as a monopoly and will each earn $1,000 in profits. However, both firms’ dominant strategy is to increase output, in which case each will earn $400 in profits.
| Hold Down Output (cooperate with other firm) | Increase Output (do not cooperate with other firm) | ||
| Hold Down Output (cooperate with other firm) | A gets $1,000, B gets $1,000 | A gets $200, B gets $1,500 | |
| Increase Output (do not cooperate with other firm) | A gets $1,500, B gets $200 | A gets $400, B gets $400 | |
Can the two firms trust each other? Consider the situation of Firm A:
- If A thinks that B will cheat on their agreement and increase output, then A will increase output, too, because for A the profit of $400 when both firms increase output (the bottom right-hand choice in Table 10.3 ) is better than a profit of only $200 if A keeps output low and B raises output (the upper right-hand choice in the table).
- If A thinks that B will cooperate by holding down output, then A may seize the opportunity to earn higher profits by raising output. After all, if B is going to hold down output, then A can earn $1,500 in profits by expanding output (the bottom left-hand choice in the table) compared with only $1,000 by holding down output as well (the upper left-hand choice in the table).
Thus, firm A will reason that it makes sense to expand output if B holds down output and that it also makes sense to expand output if B raises output. Again, B faces a parallel set of decisions that will lead B also to expand output.
The result of this prisoner’s dilemma is often that even though A and B could make the highest combined profits by cooperating in producing a lower level of output and acting like a monopolist, the two firms may well end up in a situation where they each increase output and earn only $400 each in profits . The following Clear It Up feature discusses one cartel scandal in particular.
What is the Lysine cartel?
Lysine, a $600 million-a-year industry, is an amino acid that farmers use as a feed additive to ensure the proper growth of swine and poultry. The primary U.S. producer of lysine is Archer Daniels Midland (ADM), but several other large European and Japanese firms are also in this market. For a time in the first half of the 1990s, the world’s major lysine producers met together in hotel conference rooms and decided exactly how much each firm would sell and what it would charge. The U.S. Federal Bureau of Investigation (FBI), however, had learned of the cartel and placed wire taps on a number of their phone calls and meetings.
From FBI surveillance tapes, following is a comment that Terry Wilson, president of the corn processing division at ADM, made to the other lysine producers at a 1994 meeting in Mona, Hawaii:
I wanna go back and I wanna say something very simple. If we’re going to trust each other, okay, and if I’m assured that I’m gonna get 67,000 tons by the year’s end, we’re gonna sell it at the prices we agreed to . . . The only thing we need to talk about there because we are gonna get manipulated by these [expletive] buyers—they can be smarter than us if we let them be smarter. . . . They [the customers] are not your friend. They are not my friend. And we gotta have ‘em, but they are not my friends. You are my friend. I wanna be closer to you than I am to any customer. Cause you can make us ... money. ... And all I wanna tell you again is let’s—let’s put the prices on the board. Let’s all agree that’s what we’re gonna do and then walk out of here and do it.
The price of lysine doubled while the cartel was in effect. Confronted by the FBI tapes, Archer Daniels Midland pled guilty in 1996 and paid a fine of $100 million. A number of top executives, both at ADM and other firms, later paid fines of up to $350,000 and were sentenced to 24–30 months in prison.
In another one of the FBI recordings, the president of Archer Daniels Midland told an executive from another competing firm that ADM had a slogan that, in his words, had “penetrated the whole company.” The company president stated the slogan this way: “Our competitors are our friends. Our customers are the enemy.” That slogan could stand as the motto of cartels everywhere.
How to Enforce Cooperation
How can parties who find themselves in a prisoner’s dilemma situation avoid the undesired outcome and cooperate with each other? The way out of a prisoner’s dilemma is to find a way to penalize those who do not cooperate.
Perhaps the easiest approach for colluding oligopolists, as you might imagine, would be to sign a contract with each other that they will hold output low and keep prices high. If a group of U.S. companies signed such a contract, however, it would be illegal. Certain international organizations, like the nations that are members of the Organization of Petroleum Exporting Countries (OPEC) , have signed international agreements to act like a monopoly, hold down output, and keep prices high so that all of the countries can make high profits from oil exports. Such agreements, however, because they fall in a gray area of international law, are not legally enforceable. If Nigeria, for example, decides to start cutting prices and selling more oil, Saudi Arabia cannot sue Nigeria in court and force it to stop.
Visit the Organization of the Petroleum Exporting Countries website and learn more about its history and how it defines itself.
Because oligopolists cannot sign a legally enforceable contract to act like a monopoly, the firms may instead keep close tabs on what other firms are producing and charging. Alternatively, oligopolists may choose to act in a way that generates pressure on each firm to stick to its agreed quantity of output.
One example of the pressure these firms can exert on one another is the kinked demand curve , in which competing oligopoly firms commit to match price cuts, but not price increases. Figure 10.5 shows this situation. Say that an oligopoly airline has agreed with the rest of a cartel to provide a quantity of 10,000 seats on the New York to Los Angeles route, at a price of $500. This choice defines the kink in the firm’s perceived demand curve. The reason that the firm faces a kink in its demand curve is because of how the other oligopolists react to changes in the firm’s price. If the oligopoly decides to produce more and cut its price, the other members of the cartel will immediately match any price cuts—and therefore, a lower price brings very little increase in quantity sold.
If one firm cuts its price to $300, it will be able to sell only 11,000 seats. However, if the airline seeks to raise prices, the other oligopolists will not raise their prices, and so the firm that raised prices will lose a considerable share of sales. For example, if the firm raises its price to $550, its sales drop to 5,000 seats sold. Thus, if oligopolists always match price cuts by other firms in the cartel, but do not match price increases, then none of the oligopolists will have a strong incentive to change prices, since the potential gains are minimal. This strategy can work like a silent form of cooperation, in which the cartel successfully manages to hold down output, increase price , and share a monopoly level of profits even without any legally enforceable agreement.
Many real-world oligopolies, prodded by economic changes, legal and political pressures, and the egos of their top executives, go through episodes of cooperation and competition. If oligopolies could sustain cooperation with each other on output and pricing, they could earn profits as if they were a single monopoly. However, each firm in an oligopoly has an incentive to produce more and grab a bigger share of the overall market; when firms start behaving in this way, the market outcome in terms of prices and quantity can be similar to that of a highly competitive market.
Tradeoffs of Imperfect Competition
Monopolistic competition is probably the single most common market structure in the U.S. economy. It provides powerful incentives for innovation, as firms seek to earn profits in the short run, while entry assures that firms do not earn economic profits in the long run. However, monopolistically competitive firms do not produce at the lowest point on their average cost curves. In addition, the endless search to impress consumers through product differentiation may lead to excessive social expenses on advertising and marketing.
Oligopoly is probably the second most common market structure. When oligopolies result from patented innovations or from taking advantage of economies of scale to produce at low average cost, they may provide considerable benefit to consumers. Oligopolies are often buffered by significant barriers to entry, which enable the oligopolists to earn sustained profits over long periods of time. Oligopolists also do not typically produce at the minimum of their average cost curves. When they lack vibrant competition, they may lack incentives to provide innovative products and high-quality service.
The task of public policy with regard to competition is to sort through these multiple realities, attempting to encourage behavior that is beneficial to the broader society and to discourage behavior that only adds to the profits of a few large companies, with no corresponding benefit to consumers. Monopoly and Antitrust Policy discusses the delicate judgments that go into this task.
Bring It Home
The temptation to defy the law.
Oligopolistic firms have been called “cats in a bag,” as this chapter mentioned. The French detergent makers chose to “cozy up” with each other. The result? An uneasy and tenuous relationship. When the Wall Street Journal reported on the matter, it wrote: “According to a statement a Henkel manager made to the [French anti-trust] commission, the detergent makers wanted ‘to limit the intensity of the competition between them and clean up the market.’ Nevertheless, by the early 1990s, a price war had broken out among them.” During the soap executives’ meetings, sometimes lasting more than four hours, the companies established complex pricing structures. “One [soap] executive recalled ‘chaotic’ meetings as each side tried to work out how the other had bent the rules.” Like many cartels, the soap cartel disintegrated due to the very strong temptation for each member to maximize its own individual profits.
How did this soap opera end? After an investigation, French antitrust authorities fined Colgate-Palmolive, Henkel, and Proctor & Gamble a total of €361 million ($484 million). A similar fate befell the icemakers. Bagged ice is a commodity, a perfect substitute, generally sold in 7- or 22-pound bags. No one cares what label is on the bag. By agreeing to carve up the ice market, control broad geographic swaths of territory, and set prices, the icemakers moved from perfect competition to a monopoly model. After the agreements, each firm was the sole supplier of bagged ice to a region. There were profits in both the long run and the short run. According to the courts: “These companies illegally conspired to manipulate the marketplace.” Fines totaled about $600,000—a steep fine considering a bag of ice sells for under $3 in most parts of the United States.
Even though it is illegal in many parts of the world for firms to set prices and carve up a market, the temptation to earn higher profits makes it extremely tempting to defy the law.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/principles-economics-3e/pages/1-introduction
- Authors: Steven A. Greenlaw, David Shapiro, Daniel MacDonald
- Publisher/website: OpenStax
- Book title: Principles of Economics 3e
- Publication date: Dec 14, 2022
- Location: Houston, Texas
- Book URL: https://openstax.org/books/principles-economics-3e/pages/1-introduction
- Section URL: https://openstax.org/books/principles-economics-3e/pages/10-2-oligopoly
© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
- Search Search Please fill out this field.
Monopoly vs. Oligopoly: What's the Difference?
:max_bytes(150000):strip_icc():format(webp)/0__mary_hall-5bfc262446e0fb005118b2a7.jpeg)
- Antitrust Laws: What They Are, How They Work, Major Examples
- Understanding Antitrust Laws
- Federal Trade Commission (FTC)
- Clayton Antitrust Act
- Sherman Antitrust Act
- Robinson-Patman Act
- How and Why Companies Become Monopolies
- Discriminating Monopoly
- Price Discrimination
- Predatory Pricing
- Bid Rigging
- Price Maker
- Monopolistic Markets
- Monopolistic Competition
- What Are the Characteristics of a Monopolistic Market?
- Monopolistic Market vs. Perfect Competition
- What are Some Examples of Monopolistic Markets?
- A History of U.S. Monopolies
- What Are the Most Famous Monopolies?
- Monopoly vs. Oligopoly CURRENT ARTICLE
- What are Current Examples of Oligopolies?
Monopoly vs. Oligopoly: An Overview
A monopoly and an oligopoly are market structures that exist when there is imperfect competition. A monopoly is when a single company produces goods with no close substitute, while an oligopoly is when a small number of relatively large companies produce similar but slightly different goods. In both cases, significant barriers to entry prevent other enterprises from competing.
A market's geographical size can determine which structure exists. One company might control an industry in a particular area with no other alternatives, though a few similar companies operate elsewhere in the country. In this case, a company may be a monopoly in one region but operate in an oligopoly market in a larger geographical area.
Key Takeaways
- A monopoly occurs when a single company that produces a product or service controls the market with no close substitute.
- In an oligopoly, two or more companies control the market, none of which can keep the others from having significant influence.
- Anti-trust laws prevent companies from engaging in unreasonable restraint of trade and transacting mergers that lessen competition.
A monopoly exists in areas where one company is the only or dominant force to sell a product or service in an industry . This gives the company enough power to keep competitors away from the marketplace. This could be due to high barriers to entry such as technology, steep capital requirements, government regulation, patents or high distribution costs.
Once a monopoly is established, lack of competition can lead the seller to charge high prices. Monopolies are price makers. This means they determine the cost at which their products are sold. These prices can be changed at any time. A monopoly also reduces available choices for buyers. The monopoly becomes a pure monopoly when there is absolutely no other substitute available.
Monopolies are allowed to exist when they benefit the consumer. In some cases, governments may step in and create the monopoly to provide specific services such as a railway, public transport or postal services. For example, the United States Postal Service enjoys a monopoly on first class mail and advertising mail, along with monopoly access to mailboxes.
The United States Postal Service enjoys a monopoly on letter carrying and access to mailboxes that is protected by the Constitution.
In an oligopoly, a group of companies (usually two or more) controls the market. However, no single company can keep the others from wielding significant influence over the industry, and they each may sell products that are slightly different.
Prices in this market are moderate because of the presence of competition. When one company sets a price, others will respond in fashion to remain competitive. For example, if one company cuts prices, other players typically follow suit. Prices are usually higher in an oligopoly than they would be in perfect competition .
Because there is no dominant force in the industry, companies may be tempted to collude with one another rather than compete, which keeps non-established players from entering the market. This cooperation makes them operate as though they were a single company.
In 2012, the U.S. Department of Justice alleged that Apple ( AAPL ) and five book publishers had engaged in collusion and price fixing for e-books. The department alleged that Apple and the publishers conspired to raise the price for e-book downloads from $9.99 to $14.99. A U.S. District Court sided with the government, a decision which was upheld on appeal.
In a free market, price fixing—even without judicial intervention—is unsustainable. If one company undermines its competition, others are forced to quickly follow. Companies that lower prices to the point where they are not profitable are unable to remain in business for long. Because of this, members of oligopolies tend to compete in terms of image and quality rather than price.
Legalities of Monopolies vs. Oligopolies
Oligopolies and monopolies can operate unencumbered in the United States unless they violate anti-trust laws. These laws cover unreasonable restraint of trade; plainly harmful acts such as price fixing, dividing markets and bid rigging; and mergers and acquisitions (M&A) that substantially lessen competition.
Without competition, companies have the power to fix prices and create product scarcity, which can lead to inferior products and services and higher costs for buyers. Anti-trust laws are in place to ensure a level playing field.
In 2017, the U.S. Department of Justice filed a civil antitrust suit to block AT&T's merger with Time Warner, arguing the acquisition would substantially lessen competition and lead to higher prices for television programming. However, a U.S. District Court judge disagreed with the government's argument and approved the merger, a decision that was upheld on appeal.
The government has several tools to fight monopolistic behavior. This includes the Sherman Antitrust Act , which prohibits unreasonable restraint of trade, and the Clayton Antitrust Act , which prohibits mergers that lessen competition and requires large companies that plan to merge to seek approval in advance. Anti-trust laws do not sanction companies that achieve monopoly status via offering a better product or service, or though uncontrollable developments such as a key competitor leaving the market.
Examples of Monopolies and Oligopolies
A company with a new or innovative product or service enjoys a monopoly until competitors emerge. Sometimes these new products are protected by law. For example, pharmaceutical companies in the U.S. are granted 20 years of exclusivity on new drugs. This is necessary due to the time and capital required to develop and bring new drugs to market. Without this protected status, firms would not be able to realize a return on their investment , and potentially beneficial research would be stifled.
Gas and electric utilities are also granted monopolies. However, these utilities are heavily regulated by state public utility commissions. Rates are often controlled, along with any rate increases the company may pass onto consumers.
Oligopolies exist throughout the business world . A handful of companies control the market for mass media and entertainment. Some of the big names include The Walt Disney Company ( DIS ), ViacomCBS ( VIAC ) and Comcast ( CMCSA ). In the music business, Universal Music Group and Warner Music Group have a tight grip on the market.
Federal Trade Commission. " The Antitrust Laws ."
U.S. Government Accountability Office. " U.S. Postal Service: Key Considerations for Potential Changes to USPS's Monopolies ," Pages 3, 4.
U.S. Department of Justice. " Justice Department Reaches Settlement with Three of the Largest Book Publishers and Continues to Litigate Against Apple Inc. and Two Other Publishers to Restore Price Competition and Reduce E-book Prices ."
U.S. Court of Appeals for the Second Circuit. " United States v. Apple Inc. ," Pages 4-19.
U.S. Department of Justice. " Justice Department Challenges AT&T/DirecTV’s Acquisition of Time Warner ."
United States Court of Appeals for the District of Columbia Circuit. " United States of America v. AT&T, Inc. Et Al ," Pages 4-34.
U.S. Food and Drug Administration. " Frequently Asked Questions on Patents and Exclusivity ."
:max_bytes(150000):strip_icc():format(webp)/duopoly.asp-final-631c9b223f7a4d7997cbe135b510ca48.png)
- Terms of Service
- Editorial Policy
- Privacy Policy
What does a dynamic oligopoly maximize? The continuous time Markov case
We analyze the question of whether the outcome of an oligopoly exploiting a nonrenewable resource can be replicated by a related monopoly, within the framework of continuous time and Markov Perfect Nash Equilibrium. We establish necessary and sufficient conditions and find explicit solutions in some cases. Also, very simple models with externalities are shown which Nash equilibrium cannot be replicated in a monopoly.
Key words and phrases:
1. introduction.
Margaret Slade established in [ 20 ] necessary and sufficient conditions for a Nash equilibrium to be the outcome of a single optimization problem, constructed on the basis of a “fictitious” objective function matching the first order necessary conditions of the original game. She focused on oligopolistic games, motivated by the question about whether individual firms with selfish objetives may behave as a single agent optimizing a single objective function. In [ 20 ] , static as well as dynamic games in discrete time were considered. See [ 10 ] , [ 11 ] for an analysis of the question within the framework of discrete time stochastic dynamic games, and [ 12 ] for a survey of results.
Recently, the continuous time case has been incorporated to the literature, as in [ 5 ] , [ 6 ] or [ 7 ] . The authors in [ 5 ] propose to construct a “fictitious” Hamiltonian function fulfilling two premises: the first order partial derivatives of the new Hamiltonian and of the original Hamiltonians of the players must coincide, and the new Hamiltonian can be written as the sum of a function (it may depend on the costate variables of the players) and the product of the dynamics of the original game with the corresponding costate variables. The authors show that, under some circumstances, the Hamiltonian potential can be the representation of the original differential game. The method in [ 5 ] can be applied to open–loop or to feedback strategies. The need for working with the costate variables of the original differential games, as well as maintaining the original dynamics, make difficult to find the expression of the fictitious payoff function of the control problem equivalent to the game. [ 6 ] and [ 7 ] set the question within the framework of open loop Nash equilibrium. A problem with open loop strategies is that Nash equilibrium is not credible in general, that is, it is not subgame perfect. 1 1 1 See [ 2 ] or [ 8 ] for excellent accounts about the impact of the information available to the players on the properties of Nash equilibrium. Here, we focus on the class of Markov strategies, where the players have access to the current value of time and state variable prior to taking decisions. The oligopolist may have incentives to deviate from the equilibrium at intermediate stages of the game. It is thus desirable to tackle the question addressed in [ 20 ] allowing the players to use Markov strategies.
It is not unreasonable to think that, as the players are more strategically sophisticated, it becomes harder to summarize their strategic behaviour into a single agent optimization problem. In fact, this is the case, as we will show along the paper. Uncorrelated payoffs can also make difficult to answer the question. In general, the more uncorrelated the players’ payoffs are, the more difficult is for a single–agent problem to be observationally equivalent to the oligopoly. For instance, we will show that in a duopoly with asymmetric externalities, there are preferences of the players that cannot be subsumed into the preferences of a unique agent 2 2 2 Note that team problems have players perfectly positively correlated and zero sum games are perfectly negatively correlated. As it was shown on Slade’s paper, these two extreme cases can be represented by preferences of a unique player.
It is worth noting that, although the fictitious monopoly version of the oligopoly game maintains the same structure, in general it has different payoff and different dynamics. The “fictitious” payoff was already in the foundational Slade’s paper 3 3 3 The construction of the fictitious payoff gave rise to the fundamental concept of potential game, see [ 16 ] . , but realizing the need of a “fictitious” dynamics, is new, to our knowledge. This is in contrast with the open loop Nash equilibrium, where the dynamics may be maintained, see [ 5 ] , [ 6 ] and [ 7 ] .
An interesting byproduct of constructing a monopoly being observationally equivalent to a given oligopoly with Markov players is that it induces a way to measure the effect of oligopoly competition on resource preservation. This is somewhat related with the tragedy of the commons phenomenon, see for instance [ 3 ] and [ 4 ] . The tragedy of the commons appears when Nash equilibrium implies higher depletion of the resource than under cooperative exploitation. There is a problem with measuring the tragedy of the commons impact: it needs comparison of Nash equilibrium with one of the Pareto optimal solutions of the game. It arises the question of which of the multiple Pareto solutions to choose for comparison. In the symmetric case, the equal–weight Pareto solution is a quite natural choice, but in the asymmetric case it seems to be not so straightforward. In the particular games that we study in this paper—oligopolies of resource extraction— we define a competition index of the oligopoly as the difference on the total extraction rate under oligopoly and the fictitious monopoly, divided by the total extraction rate under oligopoly. The higher the value of the index, the higher the level of competition for the resource among oligopolist due to uncorrelated objectives. For instance, in a symmetric oligopoly of resource extraction of N 𝑁 N italic_N players and without externalities, the index is
With β = 1 𝛽 1 \beta=1 italic_β = 1 (no externality), the expression above for CI is recovered, whilst β > 1 𝛽 1 \beta>1 italic_β > 1 ( 0 < β < 1 0 𝛽 1 0<\beta<1 0 < italic_β < 1 ) means that the externality is negative (positive). Note that when α = β 𝛼 𝛽 \alpha=\beta italic_α = italic_β , the index equals 0, meaning that the extraction effort is the same in the oligopoly and in the equivalent monopoly. For other values of α 𝛼 \alpha italic_α and β 𝛽 \beta italic_β , the competition strength in the oligopoly depends on the number of players N 𝑁 N italic_N and on α 𝛼 \alpha italic_α and β 𝛽 \beta italic_β .
The organization of the paper is as follows. In Section 2 we establish the framework where we develop our results, that consists of a differential game with N 𝑁 N italic_N players, smooth data and no constraints—or with constraints, but with interior Nash equilibrium—. In Section 3 we set a control problem of the same structure that may be capable of rationalizing the differential game. In Section 4, we focus on oligopolies of extraction of a nonrenewable resource with externalities. Theorem 1 in Section 5 shows that the symmetric oligopoly is always reproducible as a monopoly, with suitable fictitious payoff, discount factor, dynamics and bequest function. Section 6 applies the results above to find explicit expressions in two different oligopoly modes, the difference being that in one of the models the market price is made explicit, whereas in the other model it is hidden into the preferences of the agents, which may show actitudes towards consumptions of the competitors, interpreted as externalities. Section 7 establishes the conclusions. The paper has three appendixes. Appendix A explains the methodology that we use in our investigation. It consists in using a system of partial differential equations obtained from the Hamilton–Jacobi–Bellman equations, characterizing directly the feedback Nash equilibrium. Appendixes B and C study asymmetric oligopolies, based on Lemma 1 in Appendix A , which establishes a necessary condition for observational equivalence in asymmetric games. This is used in Appendix B to solve the problem with a duopoly with multiplicative preferences with externalities, in an infinite horizon. Appendix C focusses on additive externalities. It is shown in Theorem 3 of this appendix that there are preferences such that the outcome cannot be replicated by a single agent problem. On the positive side, sufficient conditions are given to make possible the representation in a particular class of duopolies of finite horizon and null discount factor.
It is important to say that along the paper it is taken for granted that in all the games studied a MPNE exists, at least, for some values of the parameters.
2. Description of the differential game, Nash Equilibrium and Hamilton–Jacobi–Bellman equations
𝑥 \partial_{x} ∂ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT denote total derivatives (or derivatives of a compound function). The superscript ⊤ top \,{}^{\top}\, start_FLOATSUPERSCRIPT ⊤ end_FLOATSUPERSCRIPT will denote the transposition .
| (1) |
with initial condition
| (2) |
The control region of i 𝑖 i italic_i th player is denoted U i ⊆ ℝ n superscript 𝑈 𝑖 superscript ℝ 𝑛 U^{i}\subseteq\mathbb{R}^{n} italic_U start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ⊆ blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT . The data ( t , x ) 𝑡 𝑥 (t,x) ( italic_t , italic_x ) is the initial node or root of a subgame, that we will identify with the subgame itself. The bequest function is the final payoff of the player when the game ends. When the time horizon is infinite, there is no bequest function in this case.
Definition 1 .
(Admissible strategies) . A strategic profile u = ( u 1 , … , u N ) 𝑢 superscript 𝑢 1 … superscript 𝑢 𝑁 \,u=(u^{1},\ldots,u^{N})\, italic_u = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT ) is called admissible if u ( s ) ∈ U 1 × ⋯ × U N 𝑢 𝑠 superscript 𝑈 1 ⋯ superscript 𝑈 𝑁 u(s)\in U^{1}\times\cdots\times U^{N} italic_u ( italic_s ) ∈ italic_U start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT × ⋯ × italic_U start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT for every s ∈ [ 0 , T ] 𝑠 0 𝑇 s\in[0,T] italic_s ∈ [ 0 , italic_T ] and
- 1 … 𝑁 i=1,\ldots,N italic_i = 1 , … , italic_N , there exists a function ϕ i : [ 0 , T ] × X ⊆ ℝ n ⟶ U i : superscript italic-ϕ 𝑖 0 𝑇 𝑋 superscript ℝ 𝑛 ⟶ superscript 𝑈 𝑖 \,\phi^{i}:[0,T]\times X\subseteq\mathbb{R}^{n}\longrightarrow U^{i}\, italic_ϕ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT : [ 0 , italic_T ] × italic_X ⊆ blackboard_R start_POSTSUPERSCRIPT italic_n end_POSTSUPERSCRIPT ⟶ italic_U start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT of class 𝒞 1 superscript 𝒞 1 \mathcal{C}^{1} caligraphic_C start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT such that u i ( s ) = ϕ i ( s , y ( s ) ) superscript 𝑢 𝑖 𝑠 superscript italic-ϕ 𝑖 𝑠 𝑦 𝑠 \,u^{i}(s)=\phi^{i}(s,y(s)) italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_s ) = italic_ϕ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_s , italic_y ( italic_s ) ) for every s ∈ [ 0 , T ] 𝑠 0 𝑇 s\in[0,T] italic_s ∈ [ 0 , italic_T ] ;
for every ( t , x ) 𝑡 𝑥 (t,x) ( italic_t , italic_x ) the system ( 1 ) with initial condition y ( t ) = x 𝑦 𝑡 𝑥 y(t)=x italic_y ( italic_t ) = italic_x admits a unique solution.
Thus, we consider feedback strategies. Let 𝒰 i superscript 𝒰 𝑖 \,{\mathcal{U}}^{i} caligraphic_U start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT be the set of this kind of admissible strategies of player i 𝑖 i italic_i and let 𝒰 = 𝒰 1 × ⋯ × 𝒰 N 𝒰 superscript 𝒰 1 ⋯ superscript 𝒰 𝑁 \,{\mathcal{U}}={\mathcal{U}}^{1}\times\cdots\times{\mathcal{U}}^{N} caligraphic_U = caligraphic_U start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT × ⋯ × caligraphic_U start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT be the set of admissible strategy profiles. If ϕ i superscript italic-ϕ 𝑖 \,\phi^{i}\, italic_ϕ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT is time independent, the corresponding control is called a stationary Markov control. To simplify the notation, we will identify u i superscript 𝑢 𝑖 u^{i} italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT with the feedback rule ϕ i superscript italic-ϕ 𝑖 \phi^{i} italic_ϕ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT .
The instantaneous utility function of player i 𝑖 i italic_i is denoted by L i superscript 𝐿 𝑖 L^{i} italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT and his or her bequest function by B i superscript 𝐵 𝑖 B^{i} italic_B start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT . Given ( t , x ) ∈ [ 0 , T ] × X 𝑡 𝑥 0 𝑇 𝑋 \,(t,x)\in[0,T]\times X\, ( italic_t , italic_x ) ∈ [ 0 , italic_T ] × italic_X and an admissible strategic profile u 𝑢 \,u italic_u , the payoff functional of each player is given by
| (3) |
with r i ≥ 0 subscript 𝑟 𝑖 0 r_{i}\geq 0 italic_r start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT ≥ 0 the discount rate. J i superscript 𝐽 𝑖 J^{i} italic_J start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT is the utility obtained by player i 𝑖 i italic_i when the games starts at ( t , x ) 𝑡 𝑥 (t,x) ( italic_t , italic_x ) and the profile of strategies is u 𝑢 u italic_u .
As said above, in the infinite horizon case the time interval is [ 0 , ∞ ) 0 [0,\infty) [ 0 , ∞ ) and the bequest function is null. In this case, if the problem is autonomous and the strategies are Markov stationary, the payoff functionals are independent of time, and the initial condition is simply x 𝑥 x italic_x , with t = 0 𝑡 0 t=0 italic_t = 0 .
The functions
are all assumed to be of class 𝒞 2 superscript 𝒞 2 \mathcal{C}^{2} caligraphic_C start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT .
In a non–cooperative setting the aim of the players is to maximize their individual payoff J i superscript 𝐽 𝑖 J^{i} italic_J start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT . Since this aspiration depends also on the strategies selected by the other players, it is generally impossible to attain. An adequate concept of solution is Nash equilibrium, which prevents unilateral deviations of the players from its recommendation of play. The Markov Perfect Nash Equilibrium (MPNE) considers optimality at every subgame ( t , x ) 𝑡 𝑥 (t,x) ( italic_t , italic_x ) .
Definition 2 .
(MPNE) . An N 𝑁 \,N italic_N -tuple of strategies u ∗ ∈ 𝒰 superscript 𝑢 𝒰 \,u^{*}\in{\mathcal{U}}\, italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ∈ caligraphic_U is called a Markov perfect Nash equilibrium if for every ( t , x ) ∈ [ 0 , T ] × X 𝑡 𝑥 0 𝑇 𝑋 \,(t,x)\in[0,T]\times X ( italic_t , italic_x ) ∈ [ 0 , italic_T ] × italic_X , for every u i ∈ 𝒰 i superscript 𝑢 𝑖 superscript 𝒰 𝑖 u^{i}\in{\mathcal{U}}^{i} italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ∈ caligraphic_U start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT
𝑖 1 … superscript 𝑢 absent 𝑁 (u^{*1},\ldots,u^{*i-1},u^{i},u^{*i+1},\ldots,u^{*N}) ( italic_u start_POSTSUPERSCRIPT ∗ 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT ∗ italic_i - 1 end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT ∗ italic_i + 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT ∗ italic_N end_POSTSUPERSCRIPT ) . Note that at an MPNE, no player has incentives to deviate unilaterally from u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , whatever the initial condition ( t , x ) 𝑡 𝑥 \,(t,x)\, ( italic_t , italic_x ) is. Let V i superscript 𝑉 𝑖 \,V^{i}\, italic_V start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT be the value function of the i 𝑖 \,i italic_i th player, that is
Under our smoothness conditions, the value functions satisfy the HJB system of PDEs
| (4) |
From this famous PDEs and upon taking derivatives, we will show in Appendix A another system of PDEs characterizing Nash equilibrium. Although this has been obtained previously in other papers by the author and collaborators, we will repeat the exercise in the appendix for convenience of the reader.
3. Question addressed in the paper and equivalent optimal control problem
The problem addressed in this paper is the following:
Given the N 𝑁 N italic_N –person noncooperative game described in the previous section
| (5) |
with MPNE u ∗ ∈ 𝒰 superscript 𝑢 𝒰 u^{*}\in\mathcal{U} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ∈ caligraphic_U , determine an optimal control problem
| (6) |
which admits u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT as optimal solution.
In OC, ℓ ℓ \ell roman_ℓ is the payoff integrand, ρ ≥ 0 𝜌 0 \rho\geq 0 italic_ρ ≥ 0 is the discount factor, f 𝑓 f italic_f is the dynamics, and b 𝑏 b italic_b is the bequest function. We exclude from the description of OC the feasible set 𝒰 = 𝒰 1 × ⋯ × 𝒰 N 𝒰 superscript 𝒰 1 ⋯ superscript 𝒰 𝑁 \mathcal{U}=\mathcal{U}^{1}\times\cdots\times\mathcal{U}^{N} caligraphic_U = caligraphic_U start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT × ⋯ × caligraphic_U start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT , as it is given in the description of the original DG, and it does not change.
Definition 3 .
We will say that the single agent decision problem OC is equivalent to the differential game DG, or that OC rationalizes the MPNE u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , if u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT is solution of both DG and OC.
The (equivalent) optimal control problem’s full description is
4. The oligopoly game
We analyze the equivalence question which motivates this paper, which has been established in Definition 3 , in the framework of a dynamic oligopoly game of resource extraction in continuous time, where the competition for a resource may be affected by consumption externalities. This means that the oligopolists have preferences defined not only on their own consumption, but also on the consumption of the other players. More specifically, oligopolist i ∈ { 1 , … , N } 𝑖 1 … 𝑁 i\in\{1,\ldots,N\} italic_i ∈ { 1 , … , italic_N } has preferences given by a utility function L i ( u i , u − i ) superscript 𝐿 𝑖 superscript 𝑢 𝑖 subscript 𝑢 𝑖 L^{i}(u^{i},u_{-i}) italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT ) , where L i superscript 𝐿 𝑖 L^{i} italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT is symmetric with respect to the consumption of the rest of the players, u − i = ( u 1 , … , u i − 1 , u i + 1 , … , , u N ) u_{-i}=(u^{1},\ldots,u^{i-1},u^{i+1},\ldots,,u^{N}) italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT italic_i - 1 end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT italic_i + 1 end_POSTSUPERSCRIPT , … , , italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT ) . Symmetry means that the consumption of the other players deserves the same preference consideration to the agent 5 5 5 The case where it matters who of the the other players is consuming the resource could be analized analogously; this requires of course N > 2 𝑁 2 N>2 italic_N > 2 . : if π u − i 𝜋 subscript 𝑢 𝑖 \pi u_{-i} italic_π italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT is a permutation of the profile u − i subscript 𝑢 𝑖 u_{-i} italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT (that is, a one-by-one exchange of the indexes of the rest of players), then L i ( u i , u − i ) = L i ( u i , π u − i ) superscript 𝐿 𝑖 superscript 𝑢 𝑖 subscript 𝑢 𝑖 superscript 𝐿 𝑖 superscript 𝑢 𝑖 𝜋 subscript 𝑢 𝑖 L^{i}(u^{i},u_{-i})=L^{i}(u^{i},\pi u_{-i}) italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT ) = italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , italic_π italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT ) . Here, u i superscript 𝑢 𝑖 u^{i} italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT is the extraction or consumption rate of a non renewable resource which stock at time t 𝑡 t italic_t is y ( t ) 𝑦 𝑡 y(t) italic_y ( italic_t ) . Thus, y ˙ = − ∑ j = 1 N u j ˙ 𝑦 superscript subscript 𝑗 1 𝑁 superscript 𝑢 𝑗 \dot{y}=-\sum_{j=1}^{N}u^{j} over˙ start_ARG italic_y end_ARG = - ∑ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT is the evolution of the resource. We wish to study whether it is possible that the MPNE of this game with possible externalities (assuming existence) is identical to a monopolistic problem with suitable preferences, discount factor, dynamics and bequest function. We assume that the utility of player i 𝑖 i italic_i , L i superscript 𝐿 𝑖 L^{i} italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , is increasing and strictly concave in own consumption, that is L u i i > 0 subscript superscript 𝐿 𝑖 superscript 𝑢 𝑖 0 L^{i}_{u^{i}}>0 italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT > 0 and L u i u i i < 0 subscript superscript 𝐿 𝑖 superscript 𝑢 𝑖 superscript 𝑢 𝑖 0 L^{i}_{u^{i}u^{i}}<0 italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT < 0 . The preferences are given by the functional
| (7) |
where r i ≥ 0 subscript 𝑟 𝑖 0 r_{i}\geq 0 italic_r start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT ≥ 0 is the discount factor and, as said above
| (8) |
The case T = ∞ 𝑇 T=\infty italic_T = ∞ is also allowed, which presupposes that there is not bequest payoff at ∞ \infty ∞ , B i ≡ 0 superscript 𝐵 𝑖 0 B^{i}\equiv 0 italic_B start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ≡ 0 .
| (9) |
| (10) |
We define E − i = 0 subscript 𝐸 𝑖 0 E_{-i}=0 italic_E start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT = 0 if N = 1 𝑁 1 N=1 italic_N = 1 . We assume that E i > 0 subscript 𝐸 𝑖 0 E_{i}>0 italic_E start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT > 0 , but the sign of E − i subscript 𝐸 𝑖 E_{-i} italic_E start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT is not fixed in advance.
In the case in which L u i u j i = 0 subscript superscript 𝐿 𝑖 superscript 𝑢 𝑖 superscript 𝑢 𝑗 0 L^{i}_{u^{i}u^{j}}=0 italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT end_POSTSUBSCRIPT = 0 for j ≠ i 𝑗 𝑖 j\neq i italic_j ≠ italic_i , E i subscript 𝐸 𝑖 E_{i} italic_E start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT is the inverse of the absolute risk aversion index of Arrow-Pratt with respect to player’s own consumption. In the general case, it can be considered as an average index risk that takes into account consumption of the other players. A similar interpretation can be given to E − i subscript 𝐸 𝑖 E_{-i} italic_E start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT , as a measure of risk about the consumption of the other players. When E − i > 0 subscript 𝐸 𝑖 0 E_{-i}>0 italic_E start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT > 0 , an increase in consumption of player j ≠ i 𝑗 𝑖 j\neq i italic_j ≠ italic_i (and thus, of any other player, given the assumption about symmetry made on L i superscript 𝐿 𝑖 L^{i} italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT about u − i subscript 𝑢 𝑖 u_{-i} italic_u start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT ) raises utility of player i 𝑖 i italic_i , implying that increasing the consumption level of the other players is a positive externality. This feature of the preferences is known in the literature as “keep up with the Joneses”, see [ 1 ] and [ 9 ] . If E − i < 0 subscript 𝐸 𝑖 0 E_{-i}<0 italic_E start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT < 0 , then consumption of the rest of agents diminishes own utility, since the marginal utility is negative, so that u j superscript 𝑢 𝑗 u^{j} italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT can be considered as a substitute good to u i superscript 𝑢 𝑖 u^{i} italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , for j ≠ i 𝑗 𝑖 j\neq i italic_j ≠ italic_i . In this case, consumption of other agents is a negative externality.
5. Construction of the equivalent control problem to the oligopoly game
Our approach to the problem rests on a system of PDEs arising as necessary conditions for solutions both of the original game and of the equivalent optimal control problem. This approach was developed in [ 15 ] , [ 17 ] , [ 19 ] for the deterministic case and [ 13 ] , [ 14 ] for stochastic problems. In the problem we study here, the only element that remains invariant both for the game and for the equivalent control problem is the solution, u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ; the rest of elements, like the payoffs, the discount factor, the dynamics and the bequest functions may change, as well as the value functions. Thus, working only with the HJB equations could be not sufficient to solve the problem, being more useful to work directly with the PDEs characterizing the MPNE, u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , which is the invariant object. The fact that two different systems of PDEs (that for the differential games and that for the control problem) admit the same solution is a strong condition that can be applied to get insights into the problem. The results that follow make extensive use of Appendix A and hence we will refer to that section of the paper most often.
Our starting point is obtain the PDE system ( 25 ) in Appendix A for the oligopoly game, by taking total derivatives in ( 26 ), noting that Γ i = L u i i superscript Γ 𝑖 subscript superscript 𝐿 𝑖 superscript 𝑢 𝑖 \Gamma^{i}=L^{i}_{u^{i}} roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT = italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT and ℋ i = L i − ( ∑ j = 1 N u j ) L u i i superscript ℋ 𝑖 superscript 𝐿 𝑖 superscript subscript 𝑗 1 𝑁 superscript 𝑢 𝑗 subscript superscript 𝐿 𝑖 superscript 𝑢 𝑖 \operatorname{\mathcal{H}}^{i}=L^{i}-(\sum_{j=1}^{N}u^{j})L^{i}_{u^{i}} caligraphic_H start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT = italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT - ( ∑ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT ) italic_L start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT for this game, see Remark 1 . The system becomes
| (11) |
First we study the symmetric game, both in the finite and the infinite horizon case. We will work out a duopoly version of the asymmetric game in the appendixes B and C .
5.1. Symmetric oligopoly game
Assume that the game is symmetric, that is
Due to the postulated symmetry, the first PDE in ( 11 ) becomes
| (12) |
where e 1 ( u ) = E 1 ( u , … , u ) subscript 𝑒 1 𝑢 subscript 𝐸 1 𝑢 … 𝑢 e_{1}(u)=E_{1}(u,\ldots,u) italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( italic_u ) = italic_E start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( italic_u , … , italic_u ) and e − 1 ( u ) = E − 1 ( u , … , u ) subscript 𝑒 1 𝑢 subscript 𝐸 1 𝑢 … 𝑢 e_{-1}(u)=E_{-1}(u,\ldots,u) italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u ) = italic_E start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u , … , italic_u ) . See equations ( 9 ) and ( 10 ). Remember that e − 1 = 0 subscript 𝑒 1 0 e_{-1}=0 italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT = 0 if N = 1 𝑁 1 N=1 italic_N = 1 .
If u 𝑢 u italic_u is also the optimal solution of a control problem with payoff ℓ ( u ) ℓ 𝑢 \ell(u) roman_ℓ ( italic_u ) , dynamics f ( u ) 𝑓 𝑢 f(u) italic_f ( italic_u ) , discount ρ 𝜌 \rho italic_ρ and bequest function b ( x ) 𝑏 𝑥 b(x) italic_b ( italic_x ) ( b 𝑏 b italic_b is needed only when the game horizon is finite), then u 𝑢 u italic_u must satisfy the FOCs ( 29 ), ( 30 ) and ( 31 ) in Appendix A , which become in this context
| (13) | ||||
| (14) |
where γ ( u ) = − ℓ ′ ( u ) f ′ ( u ) 𝛾 𝑢 superscript ℓ ′ 𝑢 superscript 𝑓 ′ 𝑢 \gamma(u)=-\frac{\ell^{\prime}(u)}{f^{\prime}(u)} italic_γ ( italic_u ) = - divide start_ARG roman_ℓ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) end_ARG start_ARG italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) end_ARG . So, comparing ( 12 ) and ( 13 ), we can identify 6 6 6 Of course, two PDEs may share the same set of solutions but still not be proportional with a non null factor. Frobenius Theorem of integrability of PDEs plays a role here; it was used in [ 18 ] and in [ 15 ] for the determination of MPNE which are at the same time Pareto optimal in deterministic games. We implement the simplest case that both equations are the same. It is worth noting that the dynamics of the equivalent monopoly is not − N u 𝑁 𝑢 -Nu - italic_N italic_u , which is the dynamics of the symmetric oligopoly game.
| (15) |
Integrating this differential equation for γ 𝛾 \gamma italic_γ , we obtain
| (16) |
where C 𝐶 C italic_C is a constant. Plugging this into the identity ℓ ′ ( u ) = − f ′ ( u ) γ ( u ) superscript ℓ ′ 𝑢 superscript 𝑓 ′ 𝑢 𝛾 𝑢 \ell^{\prime}(u)=-f^{\prime}(u)\gamma(u) roman_ℓ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) = - italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) italic_γ ( italic_u ) and integrating by parts
Thus, we have found a triplet OC = ( ℓ , ρ , f ) absent ℓ 𝜌 𝑓 =(\ell,\rho,f) = ( roman_ℓ , italic_ρ , italic_f ) that is a candidate to rationalize the MPNE u ∗ superscript 𝑢 u^{*} italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT in the infinite horizon case. Any ρ > 0 𝜌 0 \rho>0 italic_ρ > 0 works, including ρ = 0 𝜌 0 \rho=0 italic_ρ = 0 in the finite horizon case. 7 7 7 A complete specification will require to check monotonicity and concavity of preferences. For this, it is useful to note that ℓ ′ ( u ) = − γ ( u ) f ′ ( u ) superscript ℓ ′ 𝑢 𝛾 𝑢 superscript 𝑓 ′ 𝑢 \ell^{\prime}(u)=-\gamma(u)f^{\prime}(u) roman_ℓ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) = - italic_γ ( italic_u ) italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) and hence ℓ ′′ ( u ) = − γ ′ ( u ) f ′ ( u ) − γ ( u ) f ′′ ( u ) superscript ℓ ′′ 𝑢 superscript 𝛾 ′ 𝑢 superscript 𝑓 ′ 𝑢 𝛾 𝑢 superscript 𝑓 ′′ 𝑢 \ell^{\prime\prime}(u)=-\gamma^{\prime}(u)f^{\prime}(u)-\gamma(u)f^{\prime% \prime}(u) roman_ℓ start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT ( italic_u ) = - italic_γ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) - italic_γ ( italic_u ) italic_f start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT ( italic_u ) and study the signs. Since this does not pose a major conceptual problem, we skip the details.
5.1.1. The case with finite horizon, T < ∞ 𝑇 T<\infty italic_T < ∞ .
When the oligopoly is of finite duration, to the triplet OC = ( ℓ , ρ , f ) absent ℓ 𝜌 𝑓 =(\ell,\rho,f) = ( roman_ℓ , italic_ρ , italic_f ) found above it is needed to incorporate a suitable bequest function, b 𝑏 b italic_b . This can be done by observing that there is a final condition for the MPNE at the terminal time T 𝑇 T italic_T , see ( 27 ) in Appendix A
| (17) |
Assuming that this system defines univocally the value of the MPNE at ( T , x ) 𝑇 𝑥 (T,x) ( italic_T , italic_x ) , we write
| (18) |
for a suitably smooth function φ i superscript 𝜑 𝑖 \varphi^{i} italic_φ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT . In the symmetric game we are analyzing in this section, φ i ≡ φ superscript 𝜑 𝑖 𝜑 \varphi^{i}\equiv\varphi italic_φ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ≡ italic_φ .
As is ( 17 ), the final condition for the equivalent control problem becomes
where b 𝑏 b italic_b is the bequest function for the control problem we are looking for. Since ℓ ′ ( u ) = − γ ( u ) f ′ ( u ) superscript ℓ ′ 𝑢 𝛾 𝑢 superscript 𝑓 ′ 𝑢 \ell^{\prime}(u)=-\gamma(u)f^{\prime}(u) roman_ℓ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) = - italic_γ ( italic_u ) italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) , and f ′ ( u ) ≠ 0 superscript 𝑓 ′ 𝑢 0 f^{\prime}(u)\neq 0 italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) ≠ 0 , we have b x ( x ) = − γ ( u ( T , x ) ) subscript 𝑏 𝑥 𝑥 𝛾 𝑢 𝑇 𝑥 b_{x}(x)=-\gamma(u(T,x)) italic_b start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ( italic_x ) = - italic_γ ( italic_u ( italic_T , italic_x ) ) . Change variable u = φ ( x ) 𝑢 𝜑 𝑥 u=\varphi(x) italic_u = italic_φ ( italic_x ) into the integral ∫ d u e 1 ( u ) 𝑑 𝑢 subscript 𝑒 1 𝑢 \int\frac{du}{e_{1}(u)} ∫ divide start_ARG italic_d italic_u end_ARG start_ARG italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( italic_u ) end_ARG to obtain
and hence from, ( 16 )
Thus, the bequest function b 𝑏 b italic_b for the equivalent control problem has derivative
A further integration recovers b 𝑏 b italic_b .
We collect the above considerations in the following theorem.
Theorem 1 .
The symmetric oligopolistic game can be rationalized as a fictitious monopolistic problem OC= ( ℓ , ρ , f , b ) ℓ 𝜌 𝑓 𝑏 (\ell,\rho,f,b) ( roman_ℓ , italic_ρ , italic_f , italic_b ) where
| (19) |
| (20) |
| (21) |
C 𝐶 C italic_C denotes a constant.
In the trivial case N = 1 𝑁 1 N=1 italic_N = 1 , obviously OC=DG. When N ≥ 2 𝑁 2 N\geq 2 italic_N ≥ 2 , the total extraction rate in the symmetric DG is N u 𝑁 𝑢 Nu italic_N italic_u , but in the fictitious monopoly, it is, according to ( 20 )
Whether U mon subscript 𝑈 mon U_{\mathrm{mon}} italic_U start_POSTSUBSCRIPT roman_mon end_POSTSUBSCRIPT is greater or smaller than N u 𝑁 𝑢 Nu italic_N italic_u depends on the sign of e 1 ( u ) − e − 1 ( u ) subscript 𝑒 1 𝑢 subscript 𝑒 1 𝑢 e_{1}(u)-e_{-1}(u) italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( italic_u ) - italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u ) . If e 1 > 0 subscript 𝑒 1 0 e_{1}>0 italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT > 0 and the externality is negative, e − 1 ( u ) < 0 subscript 𝑒 1 𝑢 0 e_{-1}(u)<0 italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u ) < 0 , then e 1 ( u ) − e − 1 ( u ) > 0 subscript 𝑒 1 𝑢 subscript 𝑒 1 𝑢 0 e_{1}(u)-e_{-1}(u)>0 italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( italic_u ) - italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u ) > 0 . In this case, U mon < N u subscript 𝑈 mon 𝑁 𝑢 U_{\mathrm{mon}}<Nu italic_U start_POSTSUBSCRIPT roman_mon end_POSTSUBSCRIPT < italic_N italic_u , meaning that the total extraction rate in the fictitious monopoly is smaller than the total extraction rate in the oligopoly. Then we can interpret that negative externalities make the competition stronger than with positive externalities. This interpretation is based on the speed rate to which the resource is depleted under the oligopoly or under fictitious monopoly play.
Definition 4 .
The Competition Index of the oligopoly is defined by 8 8 8 Although this definition is placed for symmetric oligopolies, it is pretty clear that it can be translated to asymmetric ones in the obvious way.
| (22) |
The higher the CI is, the more intense the competition in the oligopoly is. We will illustrate this index with examples in Section 6.2 .
6. Applications
In this section we apply Theorem 1 above to two different formulations of the oligopoly. In the first one, the market price of the resource is given by an inverse demand function, whereas in the second formulation, the oligopolist gets utility from the use of the resource, without being apparent a price. This utility may be affected by the other oligopolists’ behavior, which we interpret as an externality. The preferences are of multiplicative type in this case.
6.1. Oligopoly pricing
Suppose that the market where the resource is traded is defined by an inverse demand function p ( Q ) 𝑝 𝑄 p(Q) italic_p ( italic_Q ) , where Q = ∑ j = 1 N u j 𝑄 superscript subscript 𝑗 1 𝑁 superscript 𝑢 𝑗 Q=\sum_{j=1}^{N}u^{j} italic_Q = ∑ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT is the total extraction effort in the industry. Suppose that the cost of extraction of the resource is c ( u i ) 𝑐 superscript 𝑢 𝑖 c(u^{i}) italic_c ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ) . Both p 𝑝 p italic_p and c 𝑐 c italic_c are smooth functions. We only consider inthe finite horizon case to keep the paper within reasonable bounds. The profit of oligopolist i 𝑖 i italic_i is
which is the integrand payoff function of the game of player i 𝑖 i italic_i . The following computations are straightforward
The oligopoly is symmetric, and thus we consider symmetric MPNE u 1 = … = u N = u superscript 𝑢 1 … superscript 𝑢 𝑁 𝑢 u^{1}=\ldots=u^{N}=u italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT = … = italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT = italic_u . Under symmetry, we have Q = N u 𝑄 𝑁 𝑢 Q=Nu italic_Q = italic_N italic_u and corresponding expressions e i ( u ) = E i ( u , … , u ) subscript 𝑒 𝑖 𝑢 subscript 𝐸 𝑖 𝑢 … 𝑢 e_{i}(u)=E_{i}(u,\ldots,u) italic_e start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT ( italic_u ) = italic_E start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT ( italic_u , … , italic_u ) , e − 1 ( u ) = E − 1 ( u , … , u ) subscript 𝑒 1 𝑢 subscript 𝐸 1 𝑢 … 𝑢 e_{-1}(u)=E_{-1}(u,\ldots,u) italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u ) = italic_E start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ( italic_u , … , italic_u ) . Theorem 1 above gives a positive answer to the observational equivalence question. To find closed form solutions suppose that p ( Q ) = A Q − q 𝑝 𝑄 𝐴 superscript 𝑄 𝑞 p(Q)=AQ^{-q} italic_p ( italic_Q ) = italic_A italic_Q start_POSTSUPERSCRIPT - italic_q end_POSTSUPERSCRIPT , where A > 0 𝐴 0 A>0 italic_A > 0 and q > 0 𝑞 0 q>0 italic_q > 0 , and eliminate costs. Then p ( Q ) = A N − q u − q 𝑝 𝑄 𝐴 superscript 𝑁 𝑞 superscript 𝑢 𝑞 p(Q)=AN^{-q}u^{-q} italic_p ( italic_Q ) = italic_A italic_N start_POSTSUPERSCRIPT - italic_q end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT - italic_q end_POSTSUPERSCRIPT and
𝑞 1 𝑁 1 𝑁 𝑞 1 k_{1}=-\frac{N}{-q-1+(N-1)(N-q-1)} italic_k start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT = - divide start_ARG italic_N end_ARG start_ARG - italic_q - 1 + ( italic_N - 1 ) ( italic_N - italic_q - 1 ) end_ARG .
Applying Theorem 1 we find
𝑁 𝑁 1 superscript 𝑞 1 subscript 𝑘 1 k_{2}=-N+(N-1)(q^{-1}-k_{1}) italic_k start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT = - italic_N + ( italic_N - 1 ) ( italic_q start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT - italic_k start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ) . Noting that
after simplifications and collection of common terms, we arrive to the expression
Thus, the fictitious monopoly consists of a market given by the inverse demand function
6.2. Multiplicative preferences with externalities
In this section we consider oligopolies where a price system is not explicitly given in the specification of the preferences of the players. Instead, we interpret rate of extraction as consumption, and preferences are given by own consumption and consumption of the rest of the players. Hence we let
Thus, the externality affecting an individual player preferences’ is multiplicative, ∏ l ≠ i k ( u l ) subscript product 𝑙 𝑖 𝑘 superscript 𝑢 𝑙 \prod_{l\neq i}k(u^{l}) ∏ start_POSTSUBSCRIPT italic_l ≠ italic_i end_POSTSUBSCRIPT italic_k ( italic_u start_POSTSUPERSCRIPT italic_l end_POSTSUPERSCRIPT ) . We obtain the derivatives
for j ≠ i 𝑗 𝑖 j\neq i italic_j ≠ italic_i . Thus
In the symmetric case that we are studying in this section, m 1 = ⋯ = m N = m subscript 𝑚 1 ⋯ subscript 𝑚 𝑁 𝑚 m_{1}=\cdots=m_{N}=m italic_m start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT = ⋯ = italic_m start_POSTSUBSCRIPT italic_N end_POSTSUBSCRIPT = italic_m . In a symmetric equilibrium u 1 = ⋯ = u N = u superscript 𝑢 1 ⋯ superscript 𝑢 𝑁 𝑢 u^{1}=\cdots=u^{N}=u italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT = ⋯ = italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT = italic_u , hence we have
where e 1 subscript 𝑒 1 e_{1} italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT and e − 1 subscript 𝑒 1 e_{-1} italic_e start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT where defined above.
6.2.1. Cobb–Douglas preferences
To get form closed solutions, let
| (23) |
Following the computations above, we obtain
Then from ( 20 )
and ℓ ( u ) ℓ 𝑢 \ell(u) roman_ℓ ( italic_u ) can be recovered easily from ( 19 ),
where m = ρ / ( η 1 r ) 𝑚 𝜌 subscript 𝜂 1 𝑟 m=\rho/(\eta_{1}r) italic_m = italic_ρ / ( italic_η start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT italic_r ) . Note that ℓ ( u ) ℓ 𝑢 \ell(u) roman_ℓ ( italic_u ) is a HARA utility with elasticity of the marginal utility m 𝑚 m italic_m .
Regarding the Competition Index ( 22 ), it is
𝛼 𝛽 1 \alpha+\beta>1 italic_α + italic_β > 1 ), CI is
It is positive when β > α 𝛽 𝛼 \beta>\alpha italic_β > italic_α and negative otherwise. Moreover, if α > 1 2 𝛼 1 2 \alpha>\frac{1}{2} italic_α > divide start_ARG 1 end_ARG start_ARG 2 end_ARG , CI increases with β 𝛽 \beta italic_β .
7. Conclusion
Nash equilibrium is not in general Pareto optimal, and thus it is not the solution of an optimal control problem which objective function is a convex combination of the player’s payoffs. It is natural then to ask whether Nash equilibrium could be the solution of a different, but related control problem, that is, whether uncoordinated play could be the outcome of cooperative play of a suitable single agent decision problem. From a philosophical point of view, if this is possible, we can interpret that the noncooperative behaviour still can be understood as cooperative in a suitable “parallel” economic world. It is intriguing that there are very simplistic oligopoly interactions for which there is no such an ideal cooperative parallel word (or fictitious monopoly). This happens when the player’s preferences are highly asymmetric and uncorrelated. This work provides a framework to analyze these kind of questions, which were originated in [ 20 ] , but within continuous time dynamic games when the players use Markov strategies.
Appendix A Technical Results
A.1. a system of partial differential equations for nash equilibrium.
To study the question addressed in the paper, that is, whether a MPNE can be attained under the the rule of a unique agent for a suitable specification of the control problem, we will resort to the characterization of the MPNE provided in Rincón-Zapatero et al. (1998) (it was afterwards extended to the non–smooth case in Rincón-Zapatero (2004) and to the stochastic case in Josa-Fombellida and Rincón-Zapatero (2007, 2015). The characterization consists in a system of PDEs for the MPNE without participation of the value functions. The quasilinear structure of the system will allow us to obtain readily important directions for analyzing the problem. In Rincón-Zapatero et al. (1998) the system for the MPNE was derived from the maximum principle. For convenience of the reader we derive it here too, but from the HJB equations.
Since we are supposing that the Nash equilibrium is interior, we have
Let us denote, for any admissible profile u 𝑢 u italic_u
| (24) |
Applying the Envelope Theorem, the derivative of max u i ∈ 𝒰 i H i ( t , x , ( u i | u − i ∗ ) , Γ k i ( x , u ∗ ) ) subscript superscript 𝑢 𝑖 superscript 𝒰 𝑖 superscript 𝐻 𝑖 𝑡 𝑥 conditional superscript 𝑢 𝑖 subscript superscript 𝑢 𝑖 subscript superscript Γ 𝑖 𝑘 𝑥 superscript 𝑢 \max_{u^{i}\in{\mathcal{U}}^{i}}H^{i}(t,x,(u^{i}|u^{*}_{-i}),\Gamma^{i}_{k}(x,% u^{*})) roman_max start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ∈ caligraphic_U start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT italic_H start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_t , italic_x , ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT | italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT - italic_i end_POSTSUBSCRIPT ) , roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ( italic_x , italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) ) is
|
|
subscript 𝑥 𝑙 subscript superscript Γ 𝑖 𝑘 \partial_{x_{k}}\Gamma^{i}_{l}=\partial_{x_{l}}\Gamma^{i}_{k} ∂ start_POSTSUBSCRIPT italic_x start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT end_POSTSUBSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT = ∂ start_POSTSUBSCRIPT italic_x start_POSTSUBSCRIPT italic_l end_POSTSUBSCRIPT end_POSTSUBSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT and thus the matrix
|
|
subscript superscript Γ 𝑖 𝑥 superscript subscript 𝑗 1 𝑁 subscript superscript Γ 𝑖 superscript 𝑢 𝑗 subscript superscript 𝑢 𝑗 𝑥 \partial_{x}\Gamma^{i}=\Gamma^{i}_{x}+\sum_{j=1}^{N}\Gamma^{i}_{u^{j}}u^{j}_{x} ∂ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT = roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT + ∑ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT end_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT . Again due to the regularity of V i superscript 𝑉 𝑖 V^{i} italic_V start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , V t x k = V x k t subscript 𝑉 𝑡 subscript 𝑥 𝑘 subscript 𝑉 subscript 𝑥 𝑘 𝑡 V_{tx_{k}}=V_{x_{k}t} italic_V start_POSTSUBSCRIPT italic_t italic_x start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT end_POSTSUBSCRIPT = italic_V start_POSTSUBSCRIPT italic_x start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT , thus
|
|
superscript subscript Γ 𝑡 𝑖 superscript subscript 𝑗 1 𝑁 subscript superscript Γ 𝑖 superscript 𝑢 𝑗 subscript superscript 𝑢 𝑗 𝑡 \partial_{t}\Gamma^{i}=\Gamma_{t}^{i}+\sum_{j=1}^{N}\Gamma^{i}_{u^{j}}u^{j}_{t} ∂ start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT = roman_Γ start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT + ∑ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT end_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT . Hence, the derivative of the HJB equations ( 4 ) with respect to x 𝑥 x italic_x is, after rearranging terms
| (25) |
Since H u i i = 0 subscript superscript 𝐻 𝑖 superscript 𝑢 𝑖 0 H^{i}_{u^{i}}=0 italic_H start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT = 0 , adding u x i ⊤ H u i i subscript superscript 𝑢 limit-from 𝑖 top 𝑥 subscript superscript 𝐻 𝑖 superscript 𝑢 𝑖 u^{i\top}_{x}H^{i}_{u^{i}} italic_u start_POSTSUPERSCRIPT italic_i ⊤ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_H start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT end_POSTSUBSCRIPT to ( 25 ) does not change the system, but allows us to write it in conservative form as follows
| (26) |
There are boundary conditions satisfied by the costate variable established by the maximum principle, p i ( T ) = B x i ( y ( T ) ) superscript 𝑝 𝑖 𝑇 subscript superscript 𝐵 𝑖 𝑥 𝑦 𝑇 p^{i}(T)=B^{i}_{x}(y(T)) italic_p start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_T ) = italic_B start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ( italic_y ( italic_T ) ) . This, and the expression obtained from the maximization of the Hamiltonian function provide a complete set of final conditions for the MPNE system ( 25 ) given by:
| (27) |
In Rincón-Zapatero et al. (1998) we show that under suitable hypotheses about the Hamiltonians, a 𝒞 1 superscript 𝒞 1 {\mathcal{C}}^{1} caligraphic_C start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT solution of ( 25 ) satisfying ( 27 ), becomes a MPNE of the differential game. That is, ( 25 ) gives not only a set of necessary conditions but also sufficient for optimality. The sufficiency result can be summarized as follows:
Theorem 2 .
| (28) |
Theorem 1 states that the costate variables of the players coincide with the gradient of the value function respect to x 𝑥 x italic_x , p i ( t ) = V x i ( t , x ) superscript 𝑝 𝑖 𝑡 subscript superscript 𝑉 𝑖 𝑥 𝑡 𝑥 \,p^{i}(t)=V^{i}_{x}(t,x) italic_p start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( italic_t ) = italic_V start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ( italic_t , italic_x ) .
As a control problem is a particular case of a game with only one player, we can deduce readily the associated PDE system for an optimal solution u 𝑢 u italic_u of a control problem with the same characteristics than the game (interior solutions, equal dimension of state and control variables). Remember that in the control problem OC= ( ℓ , ρ , f , b ) ℓ 𝜌 𝑓 𝑏 (\ell,\rho,f,b) ( roman_ℓ , italic_ρ , italic_f , italic_b ) , ℓ ℓ \ell roman_ℓ denotes the integrand, f 𝑓 f italic_f the dynamics, ρ 𝜌 \rho italic_ρ the discount factor and b 𝑏 b italic_b the bequest function; let
| (29) |
be the Hamiltonian. Since the optimal control is interior, h u = 0 subscript ℎ 𝑢 0 h_{u}=0 italic_h start_POSTSUBSCRIPT italic_u end_POSTSUBSCRIPT = 0 , and this condition serves to define
| (30) |
the vector of coestate variables. Note that p ( t ) 𝑝 𝑡 p(t) italic_p ( italic_t ) equals γ ( t , x ( t ) , u ( t , x ( t ) ) \gamma(t,x(t),u(t,x(t)) italic_γ ( italic_t , italic_x ( italic_t ) , italic_u ( italic_t , italic_x ( italic_t ) ) , where x ( t ) 𝑥 𝑡 x(t) italic_x ( italic_t ) denotes the trajectory obtained by using the feedback control u 𝑢 u italic_u . Also, let ρ ≥ 0 𝜌 0 \rho\geq 0 italic_ρ ≥ 0 be the discount factor. The PDE system ( 25 ) becomes
| (31) |
subscript superscript 𝑢 𝑗 𝑡 subscript superscript 𝑢 𝑗 𝑥 𝑓 \sum_{j\neq i}^{N}\Gamma^{i}_{u^{j}}(u^{j}_{t}+u^{j}_{x}f) ∑ start_POSTSUBSCRIPT italic_j ≠ italic_i end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT end_POSTSUBSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT + italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_f ) , which are not present in ( 31 ). They are a consequence of the game interaction.
A.2. A necessary condition for equivalence
Recall that in our problem, given the game, we want to determine, if possible, a control problem with a similar structure where the profile of strategies u = ( u 1 , … , u N ) 𝑢 superscript 𝑢 1 … superscript 𝑢 𝑁 u=(u^{1},\ldots,u^{N}) italic_u = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT ) is the solution. By a “similar structure”, we mean that the dimension of the state variable is the same as the one of the game, that is, n 𝑛 n italic_n , and that the number of controls is N × n 𝑁 𝑛 N\times n italic_N × italic_n , which the total number of strategies of the game. However, we are free to choose both the dynamics and payoff functional, and even the discount factor, but within the class of functions that respect the game model. We will be more explicit about this in what follows. hus, we face an hypothetical control problem with N × n 𝑁 𝑛 N\times n italic_N × italic_n control variables, but only n 𝑛 n italic_n state variables. This does not fit into the framework where we have found ( 31 ). However, admitting, as we do, that an optimal solution exists, still we can find a PDE for the optimal control. Note that from the first order necessary condition for the Hamiltonian h ℎ h italic_h
or, in terms of the vector functions γ i superscript 𝛾 𝑖 \gamma^{i} italic_γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT defined above,
| (32) |
at the optimal u = u ∗ 𝑢 superscript 𝑢 u=u^{*} italic_u = italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT . The next result shows conditions when ( 32 ) defines locally N − 1 𝑁 1 N-1 italic_N - 1 functions which depend smoothly on x 𝑥 x italic_x and on the controls of on of the players. Without loss of generality we choose u 1 superscript 𝑢 1 u^{1} italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT . In fact, along the text we will suppose that the aforementioned functions are globally defined.
Suppose that the n × N 𝑛 𝑁 n\times N italic_n × italic_N vector u = u ∗ 𝑢 superscript 𝑢 u=u^{*} italic_u = italic_u start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT is a solution of the optimal control problem described above with n 𝑛 n italic_n state variables. Then, if the n ( N − 1 ) × n ( N − 1 ) 𝑛 𝑁 1 𝑛 𝑁 1 n(N-1)\times n(N-1) italic_n ( italic_N - 1 ) × italic_n ( italic_N - 1 ) determinant
is not zero, then ( 32 ) defines a smooth solution
This lemma implies that the system ( 25 ) is overdetermined for u 1 superscript 𝑢 1 u^{1} italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ( n × N 𝑛 𝑁 n\times N italic_n × italic_N PDEs for only n 𝑛 n italic_n unknowns u 1 superscript 𝑢 1 u^{1} italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ), which of course, impose certain limitations in the functions and elements that define the game. This is better observed in a class of scalar games with finite horizon and no explicit dependence with respect to the state variable, which is going to be analyzed in the following section.
A.3. Scalar game with no explicit dependence on time nor on the state variable, with finite horizon and null discount
Let a game DG as in ( 5 ) with n = 1 𝑛 1 n=1 italic_n = 1 , that is X ⊆ ℝ 𝑋 ℝ X\subseteq\mathbb{R} italic_X ⊆ blackboard_R . Assume that Γ u = ( Γ u j i ) subscript Γ 𝑢 subscript superscript Γ 𝑖 superscript 𝑢 𝑗 \Gamma_{u}=(\Gamma^{i}_{u^{j}}) roman_Γ start_POSTSUBSCRIPT italic_u end_POSTSUBSCRIPT = ( roman_Γ start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT end_POSTSUBSCRIPT ) is invertible. As we are supposing that n = 1 𝑛 1 n=1 italic_n = 1 , the system ( 25 ) can be written
| (33) |
The following result is well known in the PDE literature. We include it here, joint with the proof, for convenience of the reader. Translated to our framework, the lemma establishes a useful necessary condition for a MPNE of a game as described above to be capable of rationalisation by a control problem. We show in the main text its implications in an oligopoly game with additive externalities.
Suppose that the system ( 33 ) admits a solution u = ( u 1 , … , u N ) 𝑢 superscript 𝑢 1 … superscript 𝑢 𝑁 u=(u^{1},\ldots,u^{N}) italic_u = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT ) , of the form u = Θ ( u 1 ) 𝑢 Θ superscript 𝑢 1 u=\Theta(u^{1}) italic_u = roman_Θ ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ) for some smooth function Θ = ( θ 1 , θ 2 , … , θ N ) Θ subscript 𝜃 1 subscript 𝜃 2 … subscript 𝜃 𝑁 \Theta=(\theta_{1},\theta_{2},\ldots,\theta_{N}) roman_Θ = ( italic_θ start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , italic_θ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT , … , italic_θ start_POSTSUBSCRIPT italic_N end_POSTSUBSCRIPT ) , with θ 1 = id subscript 𝜃 1 id \theta_{1}=\operatorname{id} italic_θ start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT = roman_id and such that u x 1 ≠ 0 subscript superscript 𝑢 1 𝑥 0 u^{1}_{x}\neq 0 italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ≠ 0 . Then,
is a right eigenvector of A 𝐴 A italic_A and u 1 superscript 𝑢 1 u^{1} italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT satisfies the quasilinear scalar PDE
where λ 𝜆 \lambda italic_λ is an eigenvalue of matrix A 𝐴 A italic_A .
Note that u t = u t 1 Θ ′ subscript 𝑢 𝑡 subscript superscript 𝑢 1 𝑡 superscript Θ ′ u_{t}=u^{1}_{t}\Theta^{\prime} italic_u start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT = italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT roman_Θ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT , and u x = u x 1 Θ ′ subscript 𝑢 𝑥 subscript superscript 𝑢 1 𝑥 superscript Θ ′ u_{x}=u^{1}_{x}\Theta^{\prime} italic_u start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT roman_Θ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT , thus plugging these identities into ( 33 ), we get
subscript superscript 𝑢 1 𝑡 𝜆 Θ superscript 𝑢 1 subscript superscript 𝑢 1 𝑥 0 u^{1}_{t}+\lambda(\Theta(u^{1}))u^{1}_{x}=0 italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT + italic_λ ( roman_Θ ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ) ) italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = 0 , where λ 𝜆 \lambda italic_λ is one of the the eigenvalues of A 𝐴 A italic_A . ∎
Along the same lines that the above result, the following one establishes a necessary condition for the coestate variables of the equivalent control problem.
holds. But this is the definition of left eigenvalue of A 𝐴 A italic_A with eigenvector f 𝑓 f italic_f . ∎
Appendix B Asymmetric oligopoly
Asymmetry makes the problem difficult to handle. For this reason, we consider ourselves to an asymmetric duopoly, N = 2 𝑁 2 N=2 italic_N = 2 , and to infinite horizon; let us denote u = u 1 𝑢 superscript 𝑢 1 u=u^{1} italic_u = italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT and v = u 2 𝑣 superscript 𝑢 2 v=u^{2} italic_v = italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT , to simplify notation. Suppose that the heterogeneity of the players is on self consumption, but they value the externality the same way. The preferences of the players are given by
Suppressing the time dependence term of the PDEs ( 11 ) for the MPNE, since we are in the infinite horizon game, the system becomes, assuming that α 1 α 2 − ( 1 − β ) 2 ≠ 0 subscript 𝛼 1 subscript 𝛼 2 superscript 1 𝛽 2 0 \alpha_{1}\alpha_{2}-(1-\beta)^{2}\neq 0 italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT - ( 1 - italic_β ) start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ≠ 0 and letting ϵ = ( α 1 α 2 − ( 1 − β ) 2 ) − 1 italic-ϵ superscript subscript 𝛼 1 subscript 𝛼 2 superscript 1 𝛽 2 1 \epsilon=(\alpha_{1}\alpha_{2}-(1-\beta)^{2})^{-1} italic_ϵ = ( italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT - ( 1 - italic_β ) start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ) start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT
| (38) | ||||
| (41) |
Lemma 1 in Section A.2 in Appendix A proves that a necessary condition for a MPNE to be the solution of an equivalent optimal control problem, is that there is a relation v = θ ( t , x , u ) 𝑣 𝜃 𝑡 𝑥 𝑢 v=\theta(t,x,u) italic_v = italic_θ ( italic_t , italic_x , italic_u ) ; in the game we are analyzing, where there is no explicit t 𝑡 t italic_t and x 𝑥 x italic_x dependence, the relation is simply v = θ ( u ) 𝑣 𝜃 𝑢 v=\theta(u) italic_v = italic_θ ( italic_u ) for suitable θ 𝜃 \theta italic_θ . Of course, when the game is symmetric, as in the previous section, θ 𝜃 \theta italic_θ is the identity, but under asymmetry, θ 𝜃 \theta italic_θ is unknown. 9 9 9 However, we prove in Appendix A that, if there is no discount factor in the game (and thus, the horizon is finite), θ 𝜃 \theta italic_θ can be nicely characterized in simple algebraic terms, see Lemma 2 . This will be illustrated in Appendix C , where we deal with the game with additive externalities. Here we continue working with Cobb–Douglas, multiplicative preferences. Plugging v = θ ( u ) 𝑣 𝜃 𝑢 v=\theta(u) italic_v = italic_θ ( italic_u ) into the above system, and given that v x = θ ′ u x subscript 𝑣 𝑥 superscript 𝜃 ′ subscript 𝑢 𝑥 v_{x}=\theta^{\prime}u_{x} italic_v start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = italic_θ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT italic_u start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , the system becomes a pair of differential equations for only one unknown, u ( x ) 𝑢 𝑥 u(x) italic_u ( italic_x ) , but where θ ( u ) 𝜃 𝑢 \theta(u) italic_θ ( italic_u ) is also unknown. The overdetermination can be used to find a differential equation for θ ( u ) 𝜃 𝑢 \theta(u) italic_θ ( italic_u ) , by eliminating u x subscript 𝑢 𝑥 u_{x} italic_u start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT . We simply take the ratio of both equations to get
subscript 𝛼 1 subscript 𝑟 2 1 𝛽 subscript 𝑟 1 \frac{-(1+\delta)+\epsilon\left(\frac{1-\beta}{1-\alpha_{2}}\right)((1-\alpha_% {2})-(1-\beta)\delta)+\epsilon\delta\left(\frac{\alpha_{2}}{1-\alpha_{1}}% \right)((1-\alpha_{1})\delta-(1-\beta))}{\epsilon\cancel{\delta}\left(\frac{% \alpha_{1}}{1-\alpha_{2}}\right)((1-\alpha_{2})-(1-\beta)\delta)-\cancel{% \delta}(1+\delta)+\epsilon\cancel{\delta}\left(\left(\frac{1-\beta}{1-\alpha_{% 1}}\right)((1-\alpha_{1})\delta-(1-\beta))\right)}=\frac{1}{\cancel{\delta}}% \left(\frac{\alpha_{2}r_{1}+(1-\beta)r_{2}}{\alpha_{1}r_{2}+(1-\beta)r_{1}}% \right). divide start_ARG - ( 1 + italic_δ ) + italic_ϵ ( divide start_ARG 1 - italic_β end_ARG start_ARG 1 - italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT end_ARG ) ( ( 1 - italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) - ( 1 - italic_β ) italic_δ ) + italic_ϵ italic_δ ( divide start_ARG italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT end_ARG start_ARG 1 - italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT end_ARG ) ( ( 1 - italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ) italic_δ - ( 1 - italic_β ) ) end_ARG start_ARG italic_ϵ cancel italic_δ ( divide start_ARG italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT end_ARG start_ARG 1 - italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT end_ARG ) ( ( 1 - italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) - ( 1 - italic_β ) italic_δ ) - cancel italic_δ ( 1 + italic_δ ) + italic_ϵ cancel italic_δ ( ( divide start_ARG 1 - italic_β end_ARG start_ARG 1 - italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT end_ARG ) ( ( 1 - italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ) italic_δ - ( 1 - italic_β ) ) ) end_ARG = divide start_ARG 1 end_ARG start_ARG cancel italic_δ end_ARG ( divide start_ARG italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT italic_r start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT + ( 1 - italic_β ) italic_r start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT end_ARG start_ARG italic_α start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT italic_r start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT + ( 1 - italic_β ) italic_r start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT end_ARG ) . Assuming values of the parameters such that a solution of this type exists, plugging it into ( 38 ), we have that an optimal control problem ( ℓ , f , ρ ) ℓ 𝑓 𝜌 (\ell,f,\rho) ( roman_ℓ , italic_f , italic_ρ ) rationalizes u 𝑢 u italic_u if, f ( u ) = ξ u 𝑓 𝑢 𝜉 𝑢 f(u)=\xi u italic_f ( italic_u ) = italic_ξ italic_u with 11 11 11 This comes from reading the first equation in the system ( 38 ), taking the coefficient of u x subscript 𝑢 𝑥 u_{x} italic_u start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , and using ( 31 ). We follow the same steps than in the symmetric case studied in the previous section.
where γ ( u ) = − ℓ ′ ( u ) f ′ ( u ) = − ℓ ′ ( u ) ξ 𝛾 𝑢 superscript ℓ ′ 𝑢 superscript 𝑓 ′ 𝑢 superscript ℓ ′ 𝑢 𝜉 \gamma(u)=-\frac{\ell^{\prime}(u)}{f^{\prime}(u)}=-\frac{\ell^{\prime}(u)}{\xi} italic_γ ( italic_u ) = - divide start_ARG roman_ℓ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) end_ARG start_ARG italic_f start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) end_ARG = - divide start_ARG roman_ℓ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u ) end_ARG start_ARG italic_ξ end_ARG . In this way, we get that the MPNE u 𝑢 u italic_u satisfies
which is the ODE for the Markov control.
subscript 𝛼 2 subscript 𝑟 1 1 𝛽 subscript 𝑟 2 \gamma(u)=Cu^{-\rho/(\alpha_{2}r_{1}+(1-\beta)r_{2})} italic_γ ( italic_u ) = italic_C italic_u start_POSTSUPERSCRIPT - italic_ρ / ( italic_α start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT italic_r start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT + ( 1 - italic_β ) italic_r start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT ) end_POSTSUPERSCRIPT and hence
where we have denoted generically different constants of integration by C 𝐶 C italic_C . It is possible to choose C 𝐶 C italic_C with a suitable sign and ρ > 0 𝜌 0 \rho>0 italic_ρ > 0 with a suitable size to get an increasing strictly concave utility function.
Appendix C Additive externalities
In this section we assume that the agents’ externality (if any) enters additively. Let
where L i o subscript 𝐿 𝑖 𝑜 L_{io} italic_L start_POSTSUBSCRIPT italic_i italic_o end_POSTSUBSCRIPT (utility from own consumption, “ o ”) and L i r subscript 𝐿 𝑖 𝑟 L_{ir} italic_L start_POSTSUBSCRIPT italic_i italic_r end_POSTSUBSCRIPT (externality caused for the rest of players, “ r ”) are suitable smooth functions. Here, player i 𝑖 i italic_i values her own consumption with utility L i o subscript 𝐿 𝑖 𝑜 L_{io} italic_L start_POSTSUBSCRIPT italic_i italic_o end_POSTSUBSCRIPT and the consumption of the rest of the players additively, with the same utility L i r subscript 𝐿 𝑖 𝑟 L_{ir} italic_L start_POSTSUBSCRIPT italic_i italic_r end_POSTSUBSCRIPT for each player. We let F ( u 1 , … , u N ) = − ∑ j = 1 N u j 𝐹 superscript 𝑢 1 … superscript 𝑢 𝑁 superscript subscript 𝑗 1 𝑁 superscript 𝑢 𝑗 F(u^{1},\ldots,u^{N})=-\sum_{j=1}^{N}u^{j} italic_F ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , … , italic_u start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT ) = - ∑ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_N end_POSTSUPERSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT .
𝐹 subscript 𝐼 𝑁 𝑁 superscript subscript Γ 𝑢 1 subscript 𝐻 𝑢 A=FI_{N\times N}+\Gamma_{u}^{-1}H_{u} italic_A = italic_F italic_I start_POSTSUBSCRIPT italic_N × italic_N end_POSTSUBSCRIPT + roman_Γ start_POSTSUBSCRIPT italic_u end_POSTSUBSCRIPT start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT italic_H start_POSTSUBSCRIPT italic_u end_POSTSUBSCRIPT is then
where E i ( u i ) = − L i o ′ ( u i ) L i o ′′ ( u i ) subscript 𝐸 𝑖 superscript 𝑢 𝑖 superscript subscript 𝐿 𝑖 𝑜 ′ superscript 𝑢 𝑖 superscript subscript 𝐿 𝑖 𝑜 ′′ superscript 𝑢 𝑖 E_{i}(u^{i})=-\frac{L_{io}^{\prime}(u^{i})}{L_{io}^{\prime\prime}(u^{i})} italic_E start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ) = - divide start_ARG italic_L start_POSTSUBSCRIPT italic_i italic_o end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ) end_ARG start_ARG italic_L start_POSTSUBSCRIPT italic_i italic_o end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ) end_ARG is the risk seeking index of Arrow-Pratt and E i j ( u i , u j ) = − L i r ′ ( u j ) L i o ′′ ( u i ) subscript 𝐸 𝑖 𝑗 superscript 𝑢 𝑖 superscript 𝑢 𝑗 superscript subscript 𝐿 𝑖 𝑟 ′ superscript 𝑢 𝑗 superscript subscript 𝐿 𝑖 𝑜 ′′ superscript 𝑢 𝑖 E_{ij}(u^{i},u^{j})=-\frac{L_{ir}^{\prime}(u^{j})}{L_{io}^{\prime\prime}(u^{i})} italic_E start_POSTSUBSCRIPT italic_i italic_j end_POSTSUBSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT ) = - divide start_ARG italic_L start_POSTSUBSCRIPT italic_i italic_r end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT ) end_ARG start_ARG italic_L start_POSTSUBSCRIPT italic_i italic_o end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ) end_ARG . Now it would be easy to obtain the PDE system for the MPNE. Let us focus on the two player case, to show that in some instances there is no equivalence of the game with a control problem. We analyze the case of finite horizon and null discount factor. We will state first some auxiliary results based on Appendix A .
Let the two person game with additive externalities and null discount described above. If
𝐹 subscript 𝐼 2 2 superscript subscript Γ 𝑢 1 subscript 𝐻 𝑢 A=FI_{2\times 2}+\Gamma_{u}^{-1}H_{u} italic_A = italic_F italic_I start_POSTSUBSCRIPT 2 × 2 end_POSTSUBSCRIPT + roman_Γ start_POSTSUBSCRIPT italic_u end_POSTSUBSCRIPT start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT italic_H start_POSTSUBSCRIPT italic_u end_POSTSUBSCRIPT admits two distinct real eigenvalues
with associated eigenspaces S ( λ ) 𝑆 𝜆 S(\lambda) italic_S ( italic_λ ) and S ( μ ) 𝑆 𝜇 S(\mu) italic_S ( italic_μ ) generated by
respectively. When
the matrix A 𝐴 A italic_A has no real eigenvalues.
Remember that a non-null vector ( x , y ) ⊤ superscript 𝑥 𝑦 top (x,y)^{\top} ( italic_x , italic_y ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT is an eigenvector of
with eigenvalue λ 𝜆 \lambda italic_λ iff det ( A − λ I 2 × 2 ) = 0 𝐴 𝜆 subscript 𝐼 2 2 0 \det(A-\lambda I_{2\times 2})=0 roman_det ( italic_A - italic_λ italic_I start_POSTSUBSCRIPT 2 × 2 end_POSTSUBSCRIPT ) = 0 and ( A − λ I 2 × 2 ) ( x , y ) ⊤ = ( 0 , 0 ) ⊤ 𝐴 𝜆 subscript 𝐼 2 2 superscript 𝑥 𝑦 top superscript 0 0 top (A-\lambda I_{2\times 2})(x,y)^{\top}=(0,0)^{\top} ( italic_A - italic_λ italic_I start_POSTSUBSCRIPT 2 × 2 end_POSTSUBSCRIPT ) ( italic_x , italic_y ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT = ( 0 , 0 ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT . Noting that
we obtain λ 𝜆 \lambda italic_λ and μ 𝜇 \mu italic_μ under the premise of the lemma. It is straightforward to find the eigenspaces for λ 𝜆 \lambda italic_λ and μ 𝜇 \mu italic_μ . For instance ( A − λ I 2 × 2 ) ( x , y ) ⊤ = ( 0 , 0 ) ⊤ 𝐴 𝜆 subscript 𝐼 2 2 superscript 𝑥 𝑦 top superscript 0 0 top (A-\lambda I_{2\times 2})(x,y)^{\top}=(0,0)^{\top} ( italic_A - italic_λ italic_I start_POSTSUBSCRIPT 2 × 2 end_POSTSUBSCRIPT ) ( italic_x , italic_y ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT = ( 0 , 0 ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT iff
from which we get the expression for the first eigenvector in the lemma. The case for μ 𝜇 \mu italic_μ is similar. ∎
Now we establish necessary conditions that an oligopoly as described in this paper, is equivalent to a monopoly problem within the same class (nonrenewable resource, no discount factor, finite horizon).
Proposition 1 .
Let the two person game with additive externality and null discount described above and let u = ( u 1 , u 2 ) 𝑢 superscript 𝑢 1 superscript 𝑢 2 u=(u^{1},u^{2}) italic_u = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ) be a MPNE. A necessary condition for u 𝑢 u italic_u to be rationalized by a monopolistic nonrenewable resource model is
| (42) |
When the above inequality is strict, the pair ( u 1 , u 2 ) superscript 𝑢 1 superscript 𝑢 2 (u^{1},u^{2}) ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ) is linked by u 2 = θ ( u 1 ) superscript 𝑢 2 𝜃 superscript 𝑢 1 u^{2}=\theta(u^{1}) italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT = italic_θ ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ) , where θ 𝜃 \theta italic_θ satisfies one of the ODEs
| (43) |
| (44) |
Moreover, the dynamics of the control problem f 𝑓 f italic_f is one of the two possibilities (the positive or the negative one below)
| (45) |
Also, the bequest functions B 1 superscript 𝐵 1 B^{1} italic_B start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT and B 2 superscript 𝐵 2 B^{2} italic_B start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT are linked as follows:
| (46) |
On the other hand, if
| (47) |
then no monopolistic nonrenewable resource model may rationalize the MPNE.
Condition ( 42 ) implies the existence of eigenvectors of the matrix A 𝐴 A italic_A by Lemma 4 and then Lemma 2 in Appendix A implies that if rationalization is possible, then u 2 = θ ( u 1 ) superscript 𝑢 2 𝜃 superscript 𝑢 1 u^{2}=\theta(u^{1}) italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT = italic_θ ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ) , with ( 1 , θ ′ ( u 1 ) ) 1 superscript 𝜃 ′ superscript 𝑢 1 (1,\theta^{\prime}(u^{1})) ( 1 , italic_θ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ) ) being one of the eigenvectors of A 𝐴 A italic_A , which must be either s λ subscript 𝑠 𝜆 s_{\lambda} italic_s start_POSTSUBSCRIPT italic_λ end_POSTSUBSCRIPT or s μ subscript 𝑠 𝜇 s_{\mu} italic_s start_POSTSUBSCRIPT italic_μ end_POSTSUBSCRIPT defined in Lemma 4 . These two possibilities lead to one of the ODEs for θ ′ superscript 𝜃 ′ \theta^{\prime} italic_θ start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT displayed in the theorem. Now, by Lemma 3 in Appendix A , f 𝑓 f italic_f must be one of the eigenvalues of A 𝐴 A italic_A , λ 𝜆 \lambda italic_λ or μ 𝜇 \mu italic_μ . 12 12 12 Observe that they are obviously different from F 𝐹 F italic_F under the hypotheses of the theorem.
Finally, ( 47 ) implies that no suitable θ 𝜃 \theta italic_θ may exist satisfying u 2 = θ ( u 1 ) superscript 𝑢 2 𝜃 superscript 𝑢 1 u^{2}=\theta(u^{1}) italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT = italic_θ ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT ) , as the matrix A 𝐴 A italic_A has no eigenvectors, thus the necessary condition for rationalizing the MPNE established in Lemma 2 does not hold. ∎
The previous result allows to identify preferences of the players that cannot be replicated in a single–agent decision problem. These preferences must show some degree of asymmetry, in the sense that at least one of the players is jealous of the achievements of the other player (or, in another interpretation, that consumption of the other player is a negative externality).
Theorem 3 .
Let the two person game with additive externality and null discount factor described above and let u = ( u 1 , u 2 ) 𝑢 superscript 𝑢 1 superscript 𝑢 2 u=(u^{1},u^{2}) italic_u = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ) be a MPNE. When the externality affecting to one of the oligopolist is negative, there are specifications of the preferences such that the game cannot be rationalized as a monopolistic nonrenewable resource model.
Thus, ( 47 ) holds, and hence by Proposition 1 , the MPNE cannot be rationalized as the solution of a monopolistic game. ∎
It is worth noting that in the problem that we are analyzing, the dynamics of the control problem should be given by λ 𝜆 \lambda italic_λ or μ 𝜇 \mu italic_μ defined in the above theorem, and not by the original F 𝐹 F italic_F . It comes as a surprise that the game cannot be put as a control problem if we insist in maintaining the original dynamics, F 𝐹 F italic_F . The only exception is when the game is a team problem, where both players have the same objective, since then H u j i = 0 subscript superscript 𝐻 𝑖 superscript 𝑢 𝑗 0 H^{i}_{u^{j}}=0 italic_H start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_u start_POSTSUPERSCRIPT italic_j end_POSTSUPERSCRIPT end_POSTSUBSCRIPT = 0 and the matrix is diagonal, with diagonal ( F , F ) 𝐹 𝐹 (F,F) ( italic_F , italic_F ) , and thus the only eigenvalue of A 𝐴 A italic_A is obviously F 𝐹 F italic_F .
The following theorem is a positive result, in the sense that it establishes conditions making possible the rationalization of the MPNE in a duopoly with additive externalities.
Theorem 4 .
Let the two person game with additive externality and null discount factor described above and let u = ( u 1 , u 2 ) 𝑢 superscript 𝑢 1 superscript 𝑢 2 u=(u^{1},u^{2}) italic_u = ( italic_u start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT , italic_u start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ) be a MPNE such that
Inequality ( 42 ) holds;
ODE ( 43 ) or ODE ( 44 ) admit a feasible solution θ ( u ) ≥ 0 𝜃 𝑢 0 \theta(u)\geq 0 italic_θ ( italic_u ) ≥ 0 ;
Identity ( 46 ) holds;
Letting f ( u ) = λ ( u , θ ( u ) ) 𝑓 𝑢 𝜆 𝑢 𝜃 𝑢 f(u)=\lambda(u,\theta(u)) italic_f ( italic_u ) = italic_λ ( italic_u , italic_θ ( italic_u ) ) or f ( u ) = μ ( u , θ ( u ) ) 𝑓 𝑢 𝜇 𝑢 𝜃 𝑢 f(u)=\mu(u,\theta(u)) italic_f ( italic_u ) = italic_μ ( italic_u , italic_θ ( italic_u ) ) , f 𝑓 f italic_f is strictly monotone and concave or convex.

COMMENTS
An oligopoly consists of a select few companies having significant influence over an industry.
What is a homogenous oligopoly? A homogenous, or undifferentiated oligopoly involves a small group of firms that all produce the same product, often in a standardized fashion.
An oligopoly is a market structure in which a few firms dominate. When a market is shared between a few firms, it is said to be highly concentrated. Although only a few firms dominate, it is possible that many small firms may also operate in the market. Some examples of oligopolies include the car industry, petrol retail, pharmaceutical ...
One approach to the analysis of oligopoly is to assume that firms in the industry collude, selecting the monopoly solution. Suppose an industry is a duopoly, an industry with two firms. Figure 11.5 "Monopoly Through Collusion" shows a case in which the two firms are identical.
10.2 Oligopoly. Learning Objectives. By the end of this section, you will be able to: Explain why and how oligopolies exist. Contrast collusion and competition. Interpret and analyze the prisoner's dilemma diagram. Evaluate the tradeoffs of imperfect competition. Many purchases that individuals make at the retail level are produced in markets ...
Oligopoly is a market structure in which a small number of firms has the large majority of market share . An oligopoly is similar to a monopoly , except that rather than one firm, two or more ...
There are three main models of oligopoly markets, and each is considered a slightly different competitive environment. The Cournot model considers firms that make an identical product and make output decisions simultaneously. The Bertrand model considers firms that make an identical product but compete on price and make their pricing decisions ...
The Emergence of Oligopoly: Sugar Refining as a Case Study Book Alfred S. Eichner 2019 Published by: Johns Hopkins University Press Funder: Mellon/NEH / Hopkins Open Publishing: Encore Editions Program: View
In this online lesson, we cover the oligopoly market structure. WHAT YOU'LL STUDY IN THIS ONLINE LESSON the characteristics of an oligopoly market structurethe construction of a kinked demand curveprice and non-price competitionthe existence of collusion and cartelshow game theory impacts on the behaviours of oligopolistic firmsAdditional teacher guidance is available at the end of this online ...
The behaviour of firms in the Australian market for toilet soaps, between I960 and I969, reveals certain interesting relationships which are significant for the study of demand, entry, proliferation of brands and that of advertising in oligopoly over time. It should be emphasized, however, that the con-.
Oligopoly. A market in which a few large firms dominate. Barriers prevent entry to the market, and there are few close substitutes for the product. Monopolistic competition. A market structure where many firms produce similar but not identical products. Perfect competition.
Oligopoly is a market structure in which only a few sellers offer similar or identical products. P. 347. Game theory is the study of how people behave in strategic situations. P. 348.
Perfect competition and monopoly are at opposite ends of the competition spectrum. A perfectly competitive market has many firms selling identical produ...
An oligopoly (from Ancient Greek ὀλίγος (olígos) 'few', and πωλέω (pōléō) 'to sell') is a market in which control over an industry lies in the hands of a few large sellers who own a dominant share of the market. Oligopolistic markets have homogenous products, few market participants, and inelastic demand for the products in ...
A combination of the barriers to entry that create monopolies and the product differentiation that characterizes monopolistic competition can create the...
Once committed to a certain quality tier, either high or low, in one product line, it is usually more costly to offer another product line in a different quality tier instead of offering it in the same tier. This paper probes the strategic implications of this combination of brand stickiness and operational complexity for duopoly competition.
Oligopoly and game theory: foundational concepts (practice) | Khan Academy. Khanmigo is now free for all US educators! Plan lessons, develop exit tickets, and so much more with our AI teaching assistant. Get it now!
SALES MAXIMIZATION AND OLIGOPOLY 95. models and the Baumol Sales Revenue Maximizing Model (SRM); that is, the price bands predicted by these models encompassed none of this industry's prices and outputs. The observed firms' prices and outputs fell midway between predicted SRM and profit maximizing equilibria.
Learn about the features and types of oligopoly, a market form where few firms dominate the industry, with examples and diagrams from Toppr.
Learn the difference between a monopoly and an oligopoly, both being economic market structures where there is imperfect competition in the market.
In the particular games that we study in this paper—oligopolies of resource extraction— we define a competition index of the oligopoly as the difference on the total extraction rate under oligopoly and the fictitious monopoly, divided by the total extraction rate under oligopoly.