Tutorial Playlist
Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability, a comprehensive look at percentile in statistics, the best guide to understand bayes theorem, everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, chi-square test.
What Is Hypothesis Testing in Statistics? Types and Examples

Understanding the Fundamentals of Arithmetic and Geometric Progression
The definitive guide to understand spearman’s rank correlation, mean squared error: overview, examples, concepts and more, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution, all you need to know about bias in statistics, a complete guide to get a grasp of time series analysis.
The Key Differences Between Z-Test Vs. T-Test
The Complete Guide to Understand Pearson's Correlation
A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, chi-squared test: key insights for statistical analysis.
Lesson 9 of 24 By Avijeet Biswal

Table of Contents
The world is constantly curious about the Chi-Square test's application in machine learning and how it makes a difference. Feature selection is a critical topic in machine learning , as you will have multiple features in line and must choose the best ones to build the model. Examining the relationship between the elements, the chi-square test aids in solving feature selection problems. This tutorial will teach you about the chi-square test types, how to perform these tests, their properties, their application, and more. Let's start!
What Is a Chi-Square Test?
The Chi-Square test is a statistical procedure for determining the difference between observed and expected data. This test can also be used to decide whether it correlates to our data's categorical variables. It helps to determine whether a difference between two categorical variables is due to chance or a relationship between them.
A chi-square test or comparable nonparametric test is required to test a hypothesis regarding the distribution of a categorical variable. Categorical variables, which indicate categories such as animals or countries, can be nominal or ordinal. They cannot have a normal distribution since they only have a few particular values.
Chi-Square Test Formula
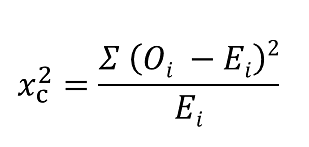
c = Degrees of freedom
O = Observed Value
E = Expected Value
The degrees of freedom in a statistical calculation represent the number of variables that can vary. The degrees of freedom can be calculated to ensure that chi-square tests are statistically valid. These tests are frequently used to compare observed data with data expected to be obtained if a particular hypothesis were true.
The Observed values are those you gather yourselves.
The expected values are the anticipated frequencies, based on the null hypothesis.
Fundamentals of Hypothesis Testing
Hypothesis testing is a technique for interpreting and drawing inferences about a population based on sample data. It aids in determining which sample data best support mutually exclusive population claims.
Null Hypothesis (H0) - The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.
H0 is the symbol for it, and it is pronounced H-naught.
Alternate Hypothesis(H1 or Ha) - The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.
Become an Expert in Data Analytics
Types of Chi-Square Tests
There are two main types of Chi-Square tests:
Independence
- Goodness-of-Fit
The Chi-Square Test of Independence is a derivable ( also known as inferential ) statistical test which examines whether the two sets of variables are likely to be related with each other or not. This test is used when we have counts of values for two nominal or categorical variables and is considered as non-parametric test. A relatively large sample size and independence of obseravations are the required criteria for conducting this test.
In a movie theatre, suppose we made a list of movie genres. Let us consider this as the first variable. The second variable is whether or not the people who came to watch those genres of movies have bought snacks at the theatre. Here the null hypothesis is that th genre of the film and whether people bought snacks or not are unrelatable. If this is true, the movie genres don’t impact snack sales.
Goodness-Of-Fit
In statistical hypothesis testing, the Chi-Square Goodness-of-Fit test determines whether a variable is likely to come from a given distribution or not. We must have a set of data values and the idea of the distribution of this data. We can use this test when we have value counts for categorical variables. This test demonstrates a way of deciding if the data values have a “ good enough” fit for our idea or if it is a representative sample data of the entire population.
Suppose we have bags of balls with five different colours in each bag. The given condition is that the bag should contain an equal number of balls of each colour. The idea we would like to test here is that the proportions of the five colours of balls in each bag must be exact.
Chi-Square Test Examples
1. Chi-Square Test for Independence
Example: A researcher wants to determine if there is an association between gender (male/female) and preference for a new product (like/dislike). The test can assess whether preferences are independent of gender.
2. Chi-Square Test for Goodness of Fit
Example: A dice manufacturer wants to test if a six-sided die is fair. They roll the die 60 times and expect each face to appear 10 times. The test checks if the observed frequencies match the expected frequencies.
3. Chi-Square Test for Homogeneity
Example: A fast-food chain wants to see if the preference for a particular menu item is consistent across different cities. The test can compare the distribution of preferences in multiple cities to see if they are homogeneous.
4. Chi-Square Test for a Contingency Table
Example: A study investigates whether smoking status (smoker/non-smoker) is related to the presence of lung disease (yes/no). The test can evaluate the relationship between smoking and lung disease in the sample.
5. Chi-Square Test for Population Proportions
Example: A political analyst wants to see if voter preference (candidate A vs. candidate B) is the same across different age groups. The test can determine if the proportions of preferences differ significantly between age groups.
How to Perform a Chi-Square Test?
Let's say you want to know if gender has anything to do with political party preference. You poll 440 voters in a simple random sample to find out which political party they prefer. The results of the survey are shown in the table below:
To see if gender is linked to political party preference, perform a Chi-Square test of independence using the steps below.
Step 1: Define the Hypothesis
H0: There is no link between gender and political party preference.
H1: There is a link between gender and political party preference.
Step 2: Calculate the Expected Values
Now you will calculate the expected frequency.
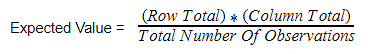
For example, the expected value for Male Republicans is:
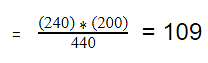
Similarly, you can calculate the expected value for each of the cells.
Step 3: Calculate (O-E)2 / E for Each Cell in the Table
Now you will calculate the (O - E)2 / E for each cell in the table.
Step 4: Calculate the Test Statistic X2
X2 is the sum of all the values in the last table
= 0.743 + 2.05 + 2.33 + 3.33 + 0.384 + 1
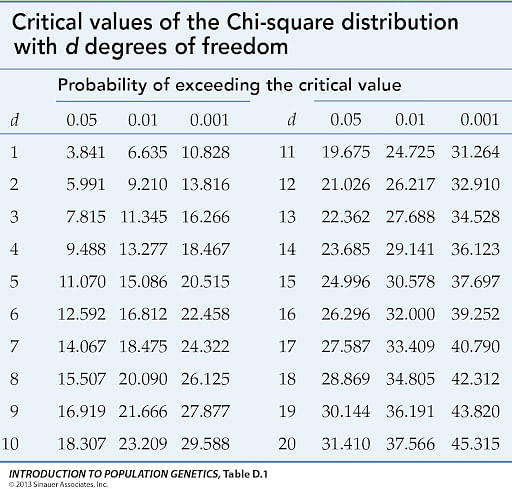
Before you can conclude, you must first determine the critical statistic, which requires determining our degrees of freedom. The degrees of freedom in this case are equal to the table's number of columns minus one multiplied by the table's number of rows minus one, or (r-1) (c-1). We have (3-1)(2-1) = 2.
Finally, you compare our obtained statistic to the critical statistic found in the chi-square table. As you can see, for an alpha level of 0.05 and two degrees of freedom, the critical statistic is 5.991, which is less than our obtained statistic of 9.83. You can reject our null hypothesis because the critical statistic is higher than your obtained statistic.
This means you have sufficient evidence to say that there is an association between gender and political party preference.
What Are Categorical Variables?
Categorical variables belong to a subset of variables that can be divided into discrete categories. Names or labels are the most common categories. These variables are also known as qualitative variables because they depict the variable's quality or characteristics.
Categorical variables can be divided into two categories:
1. Nominal Variable: A nominal variable's categories have no natural ordering. Example: Gender, Blood groups
2. Ordinal Variable: A variable that allows the categories to be sorted is an ordinal variable. An example is customer satisfaction (Excellent, Very Good, Good, Average, Bad, and so on).
Chi-Square Practice Problems
1. voting patterns.
A researcher wants to know if voting preferences (party A, party B, or party C) and gender (male, female) are related. Apply a chi-square test to the following set of data:
- Male: Party A - 30, Party B - 20, Party C - 50
- Female: Party A - 40, Party B - 30, Party C - 30
To determine if gender influences voting preferences, run a chi-square test of independence.
2. State of Health
In a sample population, a medical study examines the association between smoking status (smoker, non-smoker) and the occurrence of lung disease (yes, no). The information is as follows:
- Smoker: Yes - 90, No - 60
- Non-smoker: Yes - 30, No - 120
To find out if smoking status is related to the incidence of lung disease, do a chi-square test.
3. Consumer Preferences
Customers are surveyed by a company to determine whether their age group (under 20, 20-40, over 40) and their preferred product category (food, apparel, or electronics) are related. The information gathered is:
- Under 20: Electronic - 50, Clothing - 30, Food - 20
- 20-40: Electronic - 60, Clothing - 70, Food - 50
- Over 40: Electronic - 30, Clothing - 40, Food - 80
Use a chi-square test to investigate the connection between product preference and age group
4. Academic Performance
An educational researcher looks at the relationship between students' success on standardized tests (pass, fail) and whether or not they participate in after-school programs. The information is as follows:
- Yes: Pass - 80, Fail - 20
- No: Pass - 50, Fail - 50
Use a chi-square test to determine if involvement in after-school programs and test scores are connected.
5. Genetic Inheritance
A geneticist investigates how a particular trait is inherited in plants and seeks to ascertain whether the expression of a trait (trait present, trait absent) and the existence of a genetic marker (marker present, marker absent) are significantly correlated. The information gathered is:
- Marker Present: Trait Present - 70, Trait Absent - 30
- Marker Absent: Trait Present - 40, Trait Absent - 60
Do a chi-square test to determine if there is a correlation between the trait's expression and the genetic marker.
How to Solve Chi-Square Problems?
1. state the hypotheses.
- Null hypothesis (H0): There is no association between the variables
- Alternative hypothesis (H1): There is an association between the variables.

2. Calculate the Expected Frequencies
- Use the formula: E=(Row Total×Column Total)Grand TotalE = \frac{(Row \ Total \times Column \ Total)}{Grand \ Total}E=Grand Total(Row Total×Column Total)
3. Compute the Chi-Square Statistic
- Use the formula: χ2=∑(O−E)2E\chi^2 = \sum \frac{(O - E)^2}{E}χ2=∑E(O−E)2, where O is the observed frequency and E is the expected frequency.
4. Determine the Degrees of Freedom (df)
- Use the formula: df=(number of rows−1)×(number of columns−1)df = (number \ of \ rows - 1) \times (number \ of \ columns - 1)df=(number of rows−1)×(number of columns−1)
5. Find the Critical Value and Compare
- Use the chi-square distribution table to find the critical value for the given df and significance level (usually 0.05).
- Compare the chi-square statistic to the critical value to decide whether to reject the null hypothesis.
These practice problems help you understand how chi-square analysis tests hypotheses and explores relationships between categorical variables in various fields.
Serious About Success? Don't Settle for Less
When to Use a Chi-Square Test?
A Chi-Square Test is used to examine whether the observed results are in order with the expected values. When the data to be analysed is from a random sample, and when the variable is the question is a categorical variable, then Chi-Square proves the most appropriate test for the same. A categorical variable consists of selections such as breeds of dogs, types of cars, genres of movies, educational attainment, male v/s female etc. Survey responses and questionnaires are the primary sources of these types of data. The Chi-square test is most commonly used for analysing this kind of data. This type of analysis is helpful for researchers who are studying survey response data. The research can range from customer and marketing research to political sciences and economics.
Chi-Square Distribution
Chi-square distributions (X2) are a type of continuous probability distribution. They're commonly utilized in hypothesis testing, such as the chi-square goodness of fit and independence tests. The parameter k, which represents the degrees of freedom, determines the shape of a chi-square distribution.
Very few real-world observations follow a chi-square distribution. Chi-square distributions aim to test hypotheses, not to describe real-world distributions. In contrast, other commonly used distributions, such as normal and Poisson distributions, may explain important things like birth weights or illness cases per year.
Chi-square distributions are excellent for hypothesis testing because of its close resemblance to the conventional normal distribution. Many essential statistical tests rely on the traditional normal distribution.
In statistical analysis , the Chi-Square distribution is used in many hypothesis tests and is determined by the parameter k degree of freedom. It belongs to the family of continuous probability distributions . The Sum of the squares of the k-independent standard random variables is called the Chi-Squared distribution. Pearson’s Chi-Square Test formula is -
Where X^2 is the Chi-Square test symbol
Σ is the summation of observations
O is the observed results
E is the expected results
The shape of the distribution graph changes with the increase in the value of k, i.e., the degree of freedom.
When k is 1 or 2, the Chi-square distribution curve is shaped like a backwards ‘J’. It means there is a high chance that X^2 becomes close to zero.
Courtesy: Scribbr
When k is greater than 2, the shape of the distribution curve looks like a hump and has a low probability that X^2 is very near to 0 or very far from 0. The distribution occurs much longer on the right-hand side and shorter on the left-hand side. The probable value of X^2 is (X^2 - 2).
When k is greater than ninety, a normal distribution is seen, approximating the Chi-square distribution.
What is the P-Value in a Chi-Square Test?
The P-Value in a Chi-Square test is a statistical measure that helps to assess the importance of your test results.
Here P denotes the probability; hence for the calculation of p-values, the Chi-Square test comes into the picture. The different p-values indicate different types of hypothesis interpretations.
- P <= 0.05 (Hypothesis interpretations are rejected)
- P>= 0.05 (Hypothesis interpretations are accepted)
The concepts of probability and statistics are entangled with Chi-Square Test. Probability is the estimation of something that is most likely to happen. Simply put, it is the possibility of an event or outcome of the sample. Probability can understandably represent bulky or complicated data. And statistics involves collecting and organising, analysing, interpreting and presenting the data.
Finding P-Value
When you run all of the Chi-square tests, you'll get a test statistic called X2. You have two options for determining whether this test statistic is statistically significant at some alpha level:
- Compare the test statistic X2 to a critical value from the Chi-square distribution table.
- Compare the p-value of the test statistic X2 to a chosen alpha level.
Test statistics are calculated by taking into account the sampling distribution of the test statistic under the null hypothesis, the sample data, and the approach which is chosen for performing the test.
The p-value will be as mentioned in the following cases.
- A lower-tailed test is specified by: P(TS ts | H0 is true) p-value = cdf (ts)
- Lower-tailed tests have the following definition: P(TS ts | H0 is true) p-value = cdf (ts)
- A two-sided test is defined as follows, if we assume that the test static distribution of H0 is symmetric about 0. 2 * P(TS |ts| | H0 is true) = 2 * (1 - cdf(|ts|))
P: probability Event
TS: Test statistic is computed observed value of the test statistic from your sample cdf(): Cumulative distribution function of the test statistic's distribution (TS)
Tools and Software for Chi-Square Analysis
Here are some commonly used tools and software for performing Chi-Square analysis:
1. SPSS (Statistical Package for the Social Sciences) is a widely used software for statistical analysis, including Chi-Square tests. It provides an easy-to-use interface for performing Chi-Square tests for independence, goodness of fit, and other statistical analyses.
2. R is a powerful open-source programming language and software environment for statistical computing. The chisq.test() function in R allows for easy conducting of Chi-Square tests.
3. The SAS suite is used for advanced analytics, including Chi-Square tests. It is often used in research and business environments for complex data analysis.
4. Microsoft Excel offers a Chi-Square test function (CHISQ.TEST) for users who prefer working within spreadsheets. It’s a good option for basic Chi-Square analysis with smaller datasets.
5. Python (with libraries like SciPy or Pandas) offers robust tools for statistical analysis. The scipy.stats.chisquare() function can be used to perform Chi-Square tests.
Properties of Chi-Square Test
- Variance is double the times the number of degrees of freedom.
- Mean distribution is equal to the number of degrees of freedom.
- When the degree of freedom increases, the Chi-Square distribution curve becomes normal.
Limitations of Chi-Square Test
There are two limitations to using the chi-square test that you should be aware of.
- The chi-square test, for starters, is extremely sensitive to sample size. Even insignificant relationships can appear statistically significant when a large enough sample is used. Keep in mind that "statistically significant" does not always imply "meaningful" when using the chi-square test.
- Be mindful that the chi-square can only determine whether two variables are related. It does not necessarily follow that one variable has a causal relationship with the other. It would require a more detailed analysis to establish causality.
Invest in Excellence, Join Our Top-Tier Program
Advanced Chi-Square Test Techniques
1. Chi-Square Test with Yates' Correction (Continuity Correction)
This technique is used in 2x2 contingency tables to reduce the Chi-Square value and correct for the overestimation of statistical significance when sample sizes are small. The correction is achieved by subtracting 0.5 from the absolute difference between each observed and expected frequency.
2. Mantel-Haenszel Chi-Square Test
This technique is used to assess the association between two variables while controlling for one or more confounding variables. It’s particularly useful in stratified analyses where the goal is to examine the relationship between variables across different strata (e.g., age groups, geographic locations).
3. Chi-Square Test for Trend (Cochran-Armitage Test)
This test is used when the categorical variable is ordinal, and you want to assess whether there is a linear trend in the proportions across the ordered groups. It’s commonly used in epidemiology to analyze trends in disease rates over time or across different exposure levels.
4. Monte Carlo Simulation for Chi-Square Test
When the sample size is very small or when expected frequencies are too low, the Chi-Square distribution may not provide accurate p-values. In such cases, Monte Carlo simulation can be used to generate an empirical distribution of the test statistic, providing a more accurate significance level.
5. Bayesian Chi-Square Test
In Bayesian statistics, the Chi-Square test can be adapted to incorporate prior knowledge or beliefs about the data. This approach is useful when existing information should influence the analysis, leading to potentially more accurate conclusions.
In this tutorial titled ‘The Complete Guide to Chi-square test’, you explored the concept of Chi-square distribution and how to find the related values. You also take a look at how the critical value and chi-square value is related to each other.
If you want to gain more insight, get a work-ready understanding of statistical concepts, and learn how to use them to get into a career in Data Analytics, our Post Graduate Program in Data Analytics in partnership with Purdue University should be your next stop. A comprehensive program with training from top practitioners and in collaboration with IBM will be all you need to kickstart your career in the field. Get started today!
1. What is the chi-square test used for?
The chi-square test is a statistical method used to determine if there is a significant association between two categorical variables. It helps researchers understand whether the observed distribution of data differs from the expected distribution, allowing them to assess whether any relationship exists between the variables being studied.
2. What is the chi-square test and its types?
The chi-square test is a statistical test used to analyze categorical data and assess the independence or association between variables. There are two main types of chi-square tests:
a) Chi-square test of independence: This test determines whether there is a significant association between two categorical variables. b) Chi-square goodness-of-fit test: This test compares the observed data to the expected data to assess how well the observed data fit the expected distribution.
3. What is the difference between t-test and chi-square?
The t-test and the chi-square test are two different statistical tests used for various data types. The t-test compares the means of two groups and is suitable for continuous numerical data. On the other hand, the chi-square test examines the association between two categorical variables and is applicable to discrete categorical data.
4. What alternatives exist to the Chi-Square Test?
Alternatives include Fisher's Exact Test for small sample sizes, the G-test for large datasets, and logistic regression for modelling categorical outcomes.
5. What is the null hypothesis for Chi-Square?
The null hypothesis states no association between the categorical variables, meaning their distributions are independent.
6. How do I handle small sample sizes in a Chi-Square Test?
Use Fisher's Exact Test or apply Yates' continuity correction in 2x2 tables for small sample sizes to reduce the risk of inaccurate results.
7. What is the appropriate way to analyze Chi-Square Test results?
Compare the calculated Chi-Square statistic with the critical value from the Chi-Square distribution table; if it's more significant, reject the null hypothesis.
8. What is the advantage of the Chi-Square Test?
The Chi-Square test is simple to calculate and applies to categorical data, making it versatile for analyzing relationships in contingency tables.
Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:
About the author.
Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.
Recommended Resources
Getting Started with Google Display Network: The Ultimate Beginner’s Guide
Sanity Testing Vs Smoke Testing: Know the Differences, Applications, and Benefits Of Each
Fundamentals of Software Testing
The Building Blocks of API Development
- PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, OPM3 and the PMI ATP seal are the registered marks of the Project Management Institute, Inc.

IMAGES
VIDEO